A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of 250.9-cm and a standard deviation of 1-cm. For shipment, 27 steel rods are bundled together. Find the probability that the average length of a randomly selected bundle of steel rods is greater than 251.1-cm. P(M > 251.1-cm) =
Q: The average weight of the leatherback sea turtle is 880 lbs with a standard deviation of 44 lbs.…
A: Given Mean=μ=880, standard deviation=σ=44 P(X>1000)=? Nahi te: According to Bartleby…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Given,Mean, μ =243.2 cmStandard deviation, σ = 1.6 cmSample size, n = 20Let X be a random variable…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: The lengths of the steel rods are normally distributed with a mean of cm and a standard deviation…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: From the given information, let X be the length of steel rods. Number of steel rods are bundled…
Q: company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Given data,Mean μ=188.1sd σ=0.8If n=5P(187.3 cm < M < 188.9 cm) = ?
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: let X: The lengths of the steel rods.X has normally distributed.X~N(μ,σ)where mean(μ)=148.4 cmand…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Given: Population mean (µ) = 103.5 Population standard deviation (σ) = 0.9 Sample size (n) = 6 In…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Let X represents the lengths of the steel rods Mean (X)=98.3 Standard deviation (X)=2.4 Therefore,…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A:
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: GivenMean(μ) =265.2standard deviation(σ)=0.9sample size(n) =19
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A:
Q: manufacturer is producing metal rods whose lengths are normally distributed with a mean of 65.0 cm…
A: Population Mean,μ = 65 Population Standard Deviation,σ = 0.3
Q: hat value does your test statistic.T take on with the sample data? hat type of probability…
A: Solution: Given information: n= 10 Sample size μ=25 Population meanx=∑xn=28810=28.8 Sample mean…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: mean=145.2cm S.D=2.2cm
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: From the given information, Consider, X be the random variable that shows the length of steel rod…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Given that X~Normal(μ=238.5 , σ=0.9) μ= 238.5 , σ= 0.9 , n= 28
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: As per our guidelines we are suppose to answer one three subparts kindly post the remaining subparts…
Q: The amounts of nicotine in a certain brand of cigarette are normally distributed with a mean of…
A: Given: mean = 0.963 grams, standard deviation = 0.312 grams. The z-score follows standard normal…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A:
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: given data, normal distribution,μ=264.5σ=1we have to find out the average length separating the…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Mean = 103.4 Standard deviation = 0.9 Sample size = 12
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: From the given information, consider X be a random variable denoting the length of the steel rods…
Q: Find the probability that the average length of a randomly selected bundle of steel rods is between…
A: The probability that the average length of a randomly selected bundle of steel rods is between…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Solution-: Given: μ=269.5, σ=2.4. n=7 Let, X= The lengths of the steel rod ∴X→ N(μ=269.5,σ2=2.42) We…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A:
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Given, Let X be the length of steel rods
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Let X be the lengths of the steel rods which follows normal distribution with mean 205.9 cm and…
Q: company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Given that The lengths of the steel rods are normally distributed with a mean of 245.7-cm and a…
Q: Find the probability that the average length of a randomly selected bundle of steel rods is greater…
A: Let X denote the lengths of steel rods. Given that X follows N(mean = 158.8, SD = 0.6).
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A:
Q: The standard deviation of the lengths of stays on international cruises is 7.3 days. The sampling…
A: The standard deviation of the lengths of stays on international cruises is 7.3 days Total Sample =70…
Q: company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Given that A company produces steel rods The lengths of steel rods are normally distributed with…
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A:
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Normal distribution
Q: Assume that an adult female is randomly selected. Suppose females have pulse rates that are normally…
A: Given: Formula: Let "X" be the female pulse rates in beats per minute.
Q: company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A:
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Formula : z = (x̄ - μₓ̄ )/σₓ̄
Q: A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of…
A: Here, mean is µ = 125.6, standard deviation is σ = 1.1, and n = 15.
Q: of 232.3-cm and a standard deviation of 1.6-cm. For shipment, 21 steel rods are bundled together.…
A: Given Data : Population Mean,μ = 232.3 Population Standard Deviation,σ = 1.6 sample size…
Q: The total annual precipitation for a region is approximately normally distributed with a mean of…
A: Given information- Population mean, µ = 1050 mm Population standard deviation, σ = 400 mm Let, X be…
A company produces steel rods. The lengths of the steel rods are
Find the probability that the average length of a randomly selected bundle of steel rods is greater than 251.1-cm.
P(M > 251.1-cm) =
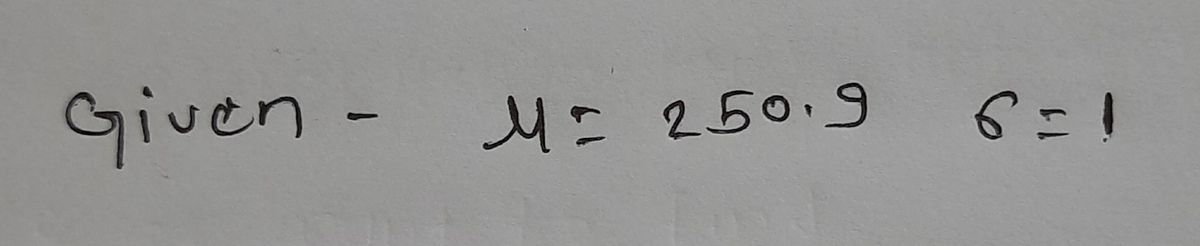
Step by step
Solved in 2 steps with 2 images
- A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of 203.7-cm and a standard deviation of 2.5-cm. For shipment, 28 steel rods are bundled together.Find the probability that the average length of a randomly selected bundle of steel rods is between 202.9-cm and 204.3-cm.PP(202.9-cm < ¯xx¯ < 204.3-cm) = Enter your answer as a number accurate to 4 decimal places.A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of 240-cm and a standard deviation of 1.4-cm. For shipment, 30 steel rods are bundled together.Find the probability that the average length of a randomly selected bundle of steel rods is less than 240.6-cm.P(M < 240.6-cm) =A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of 99.3-cm and a standard deviation of 1.5-cm. For shipment, 25 steel rods are bundled together.Find P27, which is the average length separating the smallest 27% bundles from the largest 73% bundles. P27 =
- A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of 217.3-cm and a standard deviation of 2.3-cm. For shipment, 15 steel rods are bundled together. Find the probability that the average length of a randomly selected bundle of steel rods is between 216.2. cm and 218.9-cm. P(216.2-cm < M 218.9-cm) - Enter your answer as a number accurate to 4 decimal places. Answers obtained using exact z-scores or z- scores rounded to 3 decimal places are accepted. Submit Question 4A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of 225.1-cm and a standard deviation of 1.4-cm. For shipment, 12 steel rods are bundled together.Find the probability that the average length of a randomly selected bundle of steel rods is between 224.1-cm and 224.6-cm. P(224.1-cm < M < 224.6-cm) = Enter your answer as a number accurate to 4 decimal places. Answers obtained using exact z-scores or z-scores rounded to 3 decimal places are accepted.A particular fruit's weights are normally distributed, with a mean of 455 grams and a standard deviation of 31 grams. If you pick 19 fruit at random, what is the probability that their mean weight will be between 434 grams and 443 grams? Use GeoGebra. Round to 4 places.
- The strength of the welds in a new manufacturing process is measured by the amount of weight needed to break the weld. The strength of the welds is normally distributed with mean 583 pounds. 30% of the welds had strength less than 500 pounds. What is the standard deviation of the strength of the welds?The mean weight of a Great Dane is 63.0 kg with a standard deviation of 2.3 kg. Suppose a researcher randomly samples 61 Great Danes and records the weights of the sampled dogs. Calculate the standard deviation of the mean, rounded to 2 decimal placesResearchers measured the data speeds for a particular smartphone carrier at 50 airports. The highest speed measured was 75.2 Mbps. The complete list of 50 data speeds has a mean of x= 15.49 Mbps and a standard deviation of s = 18.83Mbps.
- A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of 157-cm and a standard deviation of 0.9-cm. For shipment, 5 steel rods are bundled together. Find the probability that the average length of a randomly selected bundle of steel rods is between 156-cm and 157.2-cm.P(156-cm < M < 157.2-cm)A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of 119.5-cm and a standard deviation of 2.2-cm. For shipment, 24 steel rods are bundled together.Find P75, which is the average length separating the smallest 75% bundles from the largest 25% bundles.P75 = -cmA company produces steel rods. The lengths of the steel rods are normally distributed with a mean of 122.7-cm and a standard deviation of 0.5-cm.Find P15, which is the length separating the shortest 15% rods from the longest 85%.P15 = -cm
