Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
A-C
show all formulas and all steps of justification. Provide proper units
![**Problem 6: Analysis of Functions for Absolute Extrema**
In this problem, we are tasked to determine which of the given functions has an absolute maximum and an absolute minimum on the interval \([0, 10]\). If a function does not satisfy the criteria for the Extreme Value Theorem, we must explain why.
**Functions:**
a) \( f(x) = \frac{\ln(x)}{x+5} \)
b) \( g(x) = \frac{x^2 - 5}{x^2 + 5} \)
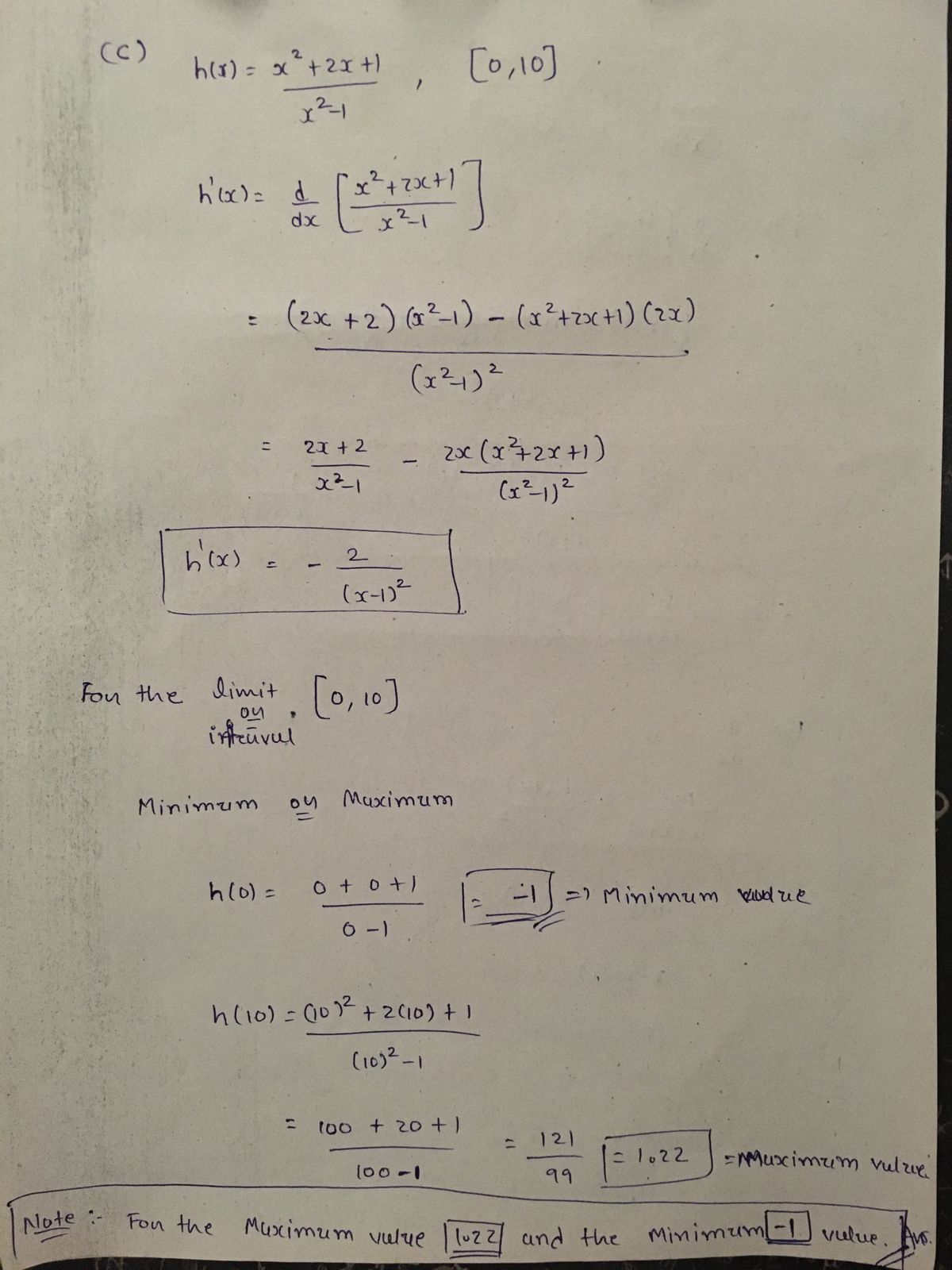
c) \( h(x) = \frac{x^2 + 2x + 1}{x^2 - 1} \)
**Guidance:**
To determine if a function has an absolute maximum and minimum on a closed interval \([a, b]\), the following conditions must be checked:
1. **Continuity:** The function must be continuous on the closed interval \([a, b]\).
2. **Closed Interval:** The interval itself must be closed, which in this case, \([0, 10]\) already is.
**Function Analysis:**
- **For \( f(x) \):** Analyze the continuity of \( f(x) = \frac{\ln(x)}{x+5} \) from \(0\) to \(10\). Particularly, check any points where \( \ln(x) \) and the denominator could cause discontinuities.
- **For \( g(x) \):** Check the continuity of \( g(x) = \frac{x^2 - 5}{x^2 + 5} \) over \([0, 10]\). Evaluate if the denominator \(x^2 + 5\) introduces any discontinuity.
- **For \( h(x) \):** Inspect \(\frac{x^2 + 2x + 1}{x^2 - 1}\) for intervals where discontinuities may occur, particularly where the denominator could become zero.
**Conclusion:**
- Possible discontinuities should be noted for functions where the denominator equals zero or where logarithmic functions are undefined (e.g., \(\ln(x)\) at \(x = 0\)). This information helps in assessing continuity and the applicability of the Extreme Value Theorem.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F70932241-1ad7-48fc-b0c5-52d574ff0aa2%2Fad7b57e0-cbd3-4cfa-8791-9c19c9d671e1%2Fo0zupgd_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem 6: Analysis of Functions for Absolute Extrema**
In this problem, we are tasked to determine which of the given functions has an absolute maximum and an absolute minimum on the interval \([0, 10]\). If a function does not satisfy the criteria for the Extreme Value Theorem, we must explain why.
**Functions:**
a) \( f(x) = \frac{\ln(x)}{x+5} \)
b) \( g(x) = \frac{x^2 - 5}{x^2 + 5} \)
c) \( h(x) = \frac{x^2 + 2x + 1}{x^2 - 1} \)
**Guidance:**
To determine if a function has an absolute maximum and minimum on a closed interval \([a, b]\), the following conditions must be checked:
1. **Continuity:** The function must be continuous on the closed interval \([a, b]\).
2. **Closed Interval:** The interval itself must be closed, which in this case, \([0, 10]\) already is.
**Function Analysis:**
- **For \( f(x) \):** Analyze the continuity of \( f(x) = \frac{\ln(x)}{x+5} \) from \(0\) to \(10\). Particularly, check any points where \( \ln(x) \) and the denominator could cause discontinuities.
- **For \( g(x) \):** Check the continuity of \( g(x) = \frac{x^2 - 5}{x^2 + 5} \) over \([0, 10]\). Evaluate if the denominator \(x^2 + 5\) introduces any discontinuity.
- **For \( h(x) \):** Inspect \(\frac{x^2 + 2x + 1}{x^2 - 1}\) for intervals where discontinuities may occur, particularly where the denominator could become zero.
**Conclusion:**
- Possible discontinuities should be noted for functions where the denominator equals zero or where logarithmic functions are undefined (e.g., \(\ln(x)\) at \(x = 0\)). This information helps in assessing continuity and the applicability of the Extreme Value Theorem.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning