A beam (ABC) has a pin support at the left-hand edge (point A) and is supported by a thinner beam (CD). Beam ABC is loaded with a linearly increasing distributed load between point A and point B. The intensity of the distributed load is zero at point A and equal to at point B. A concentrated moment, Mc, is applied to beam ABC at point C. As the connection at point C is considered pinned, there is no transfer of bending moments between beam ABC and beam CD. Beam CD is pinned at one end (Point D) and connected to beam ABC via a pin (point C). There is a concentrated load, P, applied to beam CD a shown below. Wo B TD = wol Mc = wol² -L/2 Figure 1: Two beam arrangement for question 1. In order to analyse this structure, you will: a) Construct the free body diagrams for the structure shown above. When constructing your FBD's you must make section cuts at point B and point C. You can represent the structure as three separate beams. Following this, construct the axial force, bending moment and shear force diagrams for each beam. Do not substitute in values for wo, Letc. Clearly label all of the key features of the shear force and bending moment diagrams (include features such as maximum values of axial force, shear force and bending moment and the locations where the values change from positive to negative).
A beam (ABC) has a pin support at the left-hand edge (point A) and is supported by a thinner beam (CD). Beam ABC is loaded with a linearly increasing distributed load between point A and point B. The intensity of the distributed load is zero at point A and equal to at point B. A concentrated moment, Mc, is applied to beam ABC at point C. As the connection at point C is considered pinned, there is no transfer of bending moments between beam ABC and beam CD. Beam CD is pinned at one end (Point D) and connected to beam ABC via a pin (point C). There is a concentrated load, P, applied to beam CD a shown below. Wo B TD = wol Mc = wol² -L/2 Figure 1: Two beam arrangement for question 1. In order to analyse this structure, you will: a) Construct the free body diagrams for the structure shown above. When constructing your FBD's you must make section cuts at point B and point C. You can represent the structure as three separate beams. Following this, construct the axial force, bending moment and shear force diagrams for each beam. Do not substitute in values for wo, Letc. Clearly label all of the key features of the shear force and bending moment diagrams (include features such as maximum values of axial force, shear force and bending moment and the locations where the values change from positive to negative).
Chapter2: Loads On Structures
Section: Chapter Questions
Problem 1P
Related questions
Question
100%

Transcribed Image Text:A beam (ABC) has a pin support at the left-hand edge (point A) and is supported by a thinner beam
(CD). Beam ABC is loaded with a linearly increasing distributed load between point A and point B.
The intensity of the distributed load is zero at point A and equal to at point B. A concentrated
moment, Mc, is applied to beam ABC at point C. As the connection at point C is considered pinned,
there is no transfer of bending moments between beam ABC and beam CD. Beam CD is pinned at
one end (Point D) and connected to beam ABC via a pin (point C). There is a concentrated load, P,
applied to beam CD a shown below.
Wo
|B
Symbol
E
Fallow
Tallow
000
L
D
P = wol
↑
L/4
L
-L/2→
Figure 1: Two beam arrangement for question 1.
Mc = wol²
In order to analyse this structure, you will:
a) Construct the free body diagrams for the structure shown above. When constructing your
FBD's you must make section cuts at point B and point C. You can represent the structure as
three separate beams. Following this, construct the axial force, bending moment and shear
force diagrams for each beam. Do not substitute in values for wo, Letc. Clearly label all of the
key features of the shear force and bending moment diagrams (include features such as
maximum values of axial force, shear force and bending moment and the locations where
the values change from positive to negative).
Take care with your sign convention!
b) Assuming that both beams (ABC and CD) have a solid square cross-section. The side lengths
of the cross-sections are 'ABC' and 'aco'. Design the beams to withstand the applied loading.
Make sure that you consider all loading conditions (axial, bending and shear). Clearly state
your calculated value of a in mm for each possible failure mode for both beams to one
decimal place. Use the parameters shown in Table 1 to calculate the beam dimensions.
5
1.5
Table 1: The material properties used in part (b) of question 1
Value
200.0
250.0
150.0
L/2
Units
GPa
MPa
MPa
kN/m
m
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 7 steps with 15 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Based on the previous result, solve second part of the question
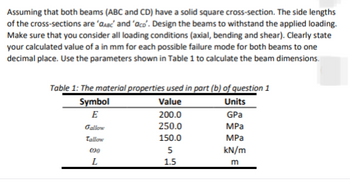
Transcribed Image Text:Assuming that both beams (ABC and CD) have a solid square cross-section. The side lengths
of the cross-sections are 'ABC' and 'aco'. Design the beams to withstand the applied loading.
Make sure that you consider all loading conditions (axial, bending and shear). Clearly state
your calculated value of a in mm for each possible failure mode for both beams to one
decimal place. Use the parameters shown in Table 1 to calculate the beam dimensions.
Table 1: The material properties used in part (b) of question 1
Value
200.0
250.0
150.0
Symbol
E
Gallow
Tallow
030
L
5
1.5
Units
GPa
MPa
MPa
kN/m
m
Solution
Follow-up Question
So VDL should belong to upward force instead of downward force side. And the sign should be negative instead of positive. Can you make it more clear ?

Transcribed Image Text:Sum of upward forces=Sum of downward forces
VA + VB + V₁ + V₂ = VB + V₁ + VDL
Vc
Cancel Vc and Vb from both sides ;
= VDL
VA + VD
But;
VDL =
xw₁ XL
So,
VA + VD =
NIF
X Wo X L
Solution
Follow-up Question
If Wo is acting upward, How could VDL act downward?
Solution
Follow-up Question
For the first line of calculation: why VA+VD= 1/2xWxL
I think it should be VA+VD=-1/2xWxL according to sign convention
Solution
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you


Structural Analysis (10th Edition)
Civil Engineering
ISBN:
9780134610672
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Principles of Foundation Engineering (MindTap Cou…
Civil Engineering
ISBN:
9781337705028
Author:
Braja M. Das, Nagaratnam Sivakugan
Publisher:
Cengage Learning


Structural Analysis (10th Edition)
Civil Engineering
ISBN:
9780134610672
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Principles of Foundation Engineering (MindTap Cou…
Civil Engineering
ISBN:
9781337705028
Author:
Braja M. Das, Nagaratnam Sivakugan
Publisher:
Cengage Learning

Fundamentals of Structural Analysis
Civil Engineering
ISBN:
9780073398006
Author:
Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel Lanning
Publisher:
McGraw-Hill Education


Traffic and Highway Engineering
Civil Engineering
ISBN:
9781305156241
Author:
Garber, Nicholas J.
Publisher:
Cengage Learning