A batter in the major leagues has a .2 batting average against left-handed pitchers and a .3 batting average against right-handed pitchers (i.e. he has a .2 and .3 probability, respectively, of getting on base). Suppose in a given season he will have 80 at bats with left-handed pitchers and 150 at-bats with right-handed pitchers. How many times should he be expected to get on a base in a given season?
Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.
A batter in the major leagues has a .2 batting average against left-handed pitchers and a .3 batting average against right-handed pitchers (i.e. he has a .2 and .3
Given Data:
The probability of batting average against the left-handed pitcher is: p=0.2
The probability of batting average against the right-handed pitcher is: u=0.3
The total number of bats with the left-hand pitcher is: n=80
The total number of bats with the right-pitcher is: m=150
Let X be the random variable of batting against left-handed pitchers, and Y be the random variable of batting against right-handed pitchers.
The expression to calculate the expected value of getting on the base in a season is,
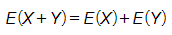
Step by step
Solved in 2 steps with 6 images




