a) an edge between vertices representing cities that have a flight between them (in either direction). b) an edge between vertices representing cities for each flight that operates between them (in either direction). c) an edge between vertices representing cities for each flight that operates between them (in either direction), plus a loop for a special sightseeing trip that takes off and lands in Miami. d) an edge from a vertex representing a city where a flight starts to the vertex representing the city where it ends. e) an edge for each flight from a vertex representing a city where the flight begins to the vertex representing the city where the flight ends.
Draw graph models, stating the type of graph (from Table 1) used, to represent airline routes where every day there are four flights from Boston to Newark, two flights from Newark to Boston, three flights from Newark to Miami, two flights from Miami to Newark, one flight from Newark to Detroit, two flights from Detroit to Newark, three flights from Newark to Washington, two flights from Washington to Newark, and one flight from Washington to Miami, with
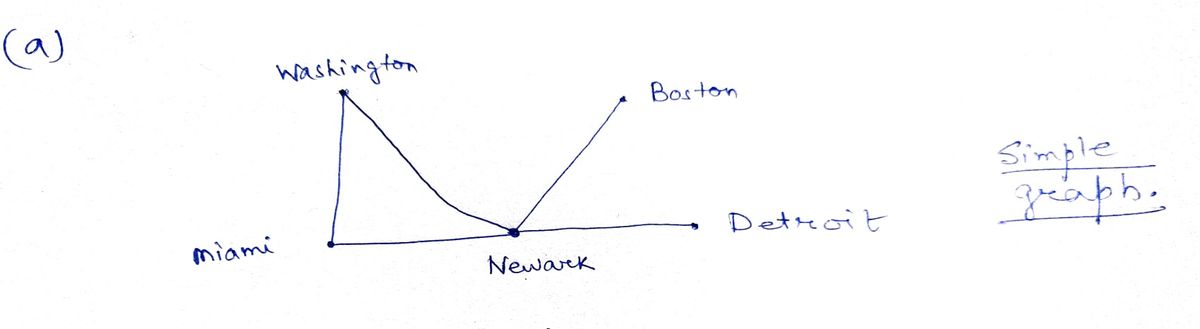
a) an edge between vertices representing cities that have a flight between them (in either direction).
b) an edge between vertices representing cities for each flight that operates between them (in either direction).
c) an edge between vertices representing cities for each flight that operates between them (in either direction), plus a loop for a special sightseeing trip that takes off and lands in Miami.
d) an edge from a vertex representing a city where a flight starts to the vertex representing the city where it ends.
e) an edge for each flight from a vertex representing a city where the flight begins to the vertex representing the city where the flight ends.

Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images









