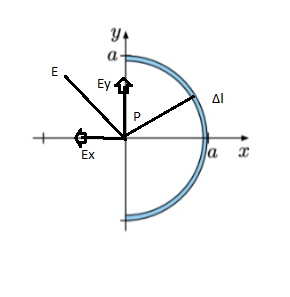
a- 8.4) Uniform arc A bent semi-circular rod of radius a carries total charge Q uniformly distributed along the rod. Compute the electric field at the origin. la

The given rod is semicircular in shape, the charges are distributed uniformly along the surface of the rod. the approach will be to calculate the electric field at small distribution, then integrating the distribution for the semicircle.
consider a small section on the rod as shown in the figure below:
let the charge distribution density be
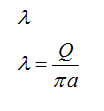
The charge contained in the small elemental length is given as: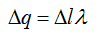
The electric field at point P is given as
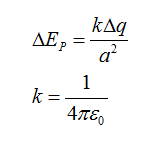
the net electric field is the sum of the horizontal and the vertical electric field. the vertical components will cancel each other while the horizontal component will be present.
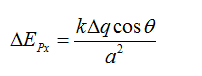
this component will be integrated to find the net electric field.
the value of the
Θ varies from -pi/2 to pi/2
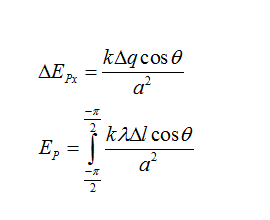
the above equation can be simplified as: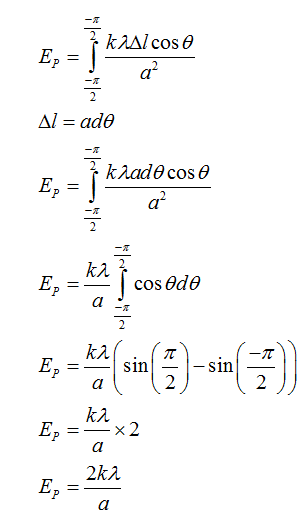
Step by step
Solved in 5 steps with 9 images









