Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
100%
I keep getting my signs wrong on this one so I was hoping someone could show me the right way!
![The image contains a mathematical expression involving vectors:
\[ \mathbf{A} = (5\hat{\imath} - 5\hat{\jmath}) \times (2x\hat{\imath} - z\hat{k}) \]
This expression represents the cross product of two vectors in three-dimensional space. The first vector is \(5\hat{\imath} - 5\hat{\jmath}\) and the second vector is \(2x\hat{\imath} - z\hat{k}\).
### Explanation:
- **Vectors:**
- \(\hat{\imath}\), \(\hat{\jmath}\), and \(\hat{k}\) are the unit vectors along the x, y, and z axes, respectively.
- The first vector \((5\hat{\imath} - 5\hat{\jmath})\) has components in the x and y directions.
- The second vector \((2x\hat{\imath} - z\hat{k})\) has components in the x and z directions.
- **Cross Product:**
- The cross product results in a vector that is perpendicular to the plane containing the two original vectors and has a magnitude equal to the product of the magnitudes of the two vectors and the sine of the angle between them.
When used in educational contexts, understanding and performing cross products is critical in physics, engineering, and computer graphics, where concepts of rotational dynamics and torque are applied.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc8854ffd-431b-44a2-b47e-daec534c3a26%2Fb8667371-93b3-4ebb-b51e-31a832019018%2Fazxkrnq_processed.jpeg&w=3840&q=75)
Transcribed Image Text:The image contains a mathematical expression involving vectors:
\[ \mathbf{A} = (5\hat{\imath} - 5\hat{\jmath}) \times (2x\hat{\imath} - z\hat{k}) \]
This expression represents the cross product of two vectors in three-dimensional space. The first vector is \(5\hat{\imath} - 5\hat{\jmath}\) and the second vector is \(2x\hat{\imath} - z\hat{k}\).
### Explanation:
- **Vectors:**
- \(\hat{\imath}\), \(\hat{\jmath}\), and \(\hat{k}\) are the unit vectors along the x, y, and z axes, respectively.
- The first vector \((5\hat{\imath} - 5\hat{\jmath})\) has components in the x and y directions.
- The second vector \((2x\hat{\imath} - z\hat{k})\) has components in the x and z directions.
- **Cross Product:**
- The cross product results in a vector that is perpendicular to the plane containing the two original vectors and has a magnitude equal to the product of the magnitudes of the two vectors and the sine of the angle between them.
When used in educational contexts, understanding and performing cross products is critical in physics, engineering, and computer graphics, where concepts of rotational dynamics and torque are applied.
Expert Solution
Step 1
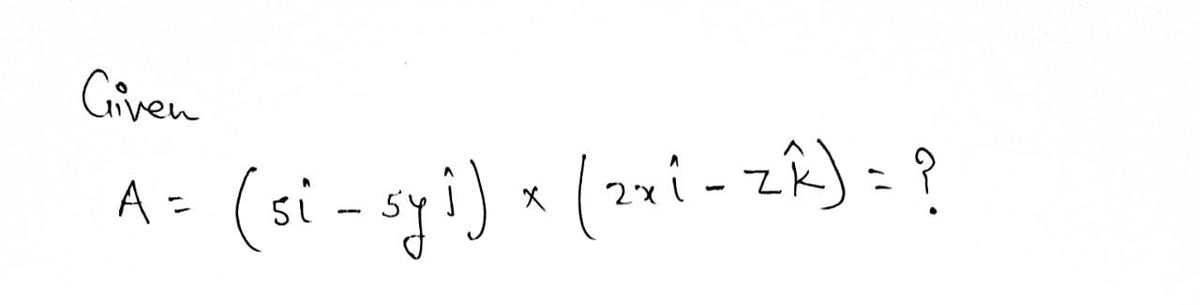
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning