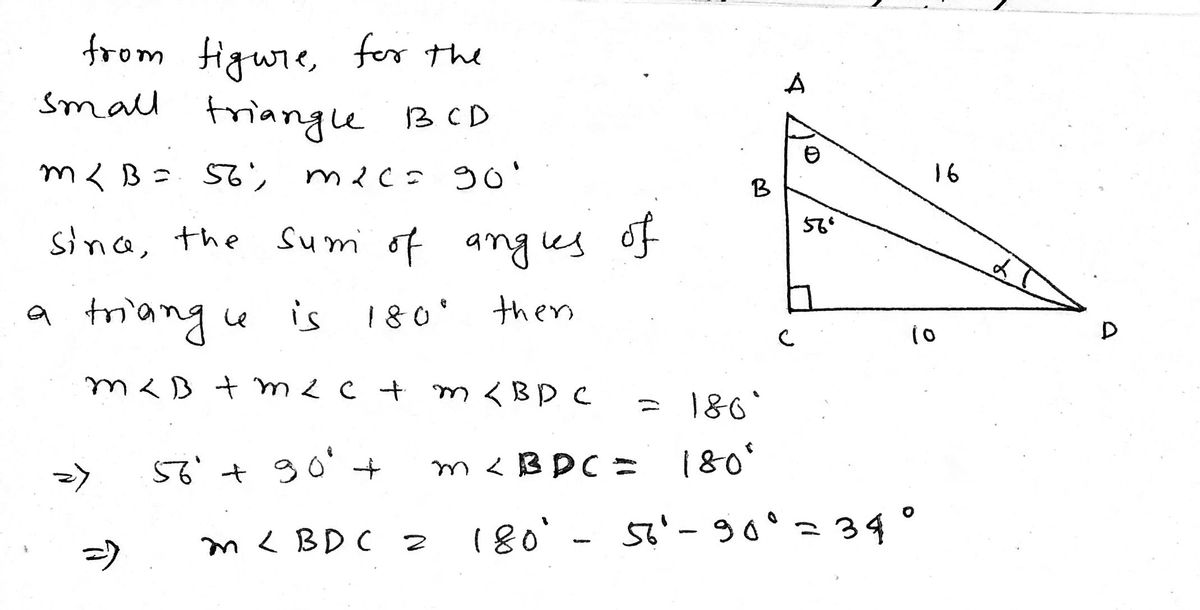Trigonometry (11th Edition) 11th Edition
ISBN: 9780134217437
Author: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
1 Trigonometric Functions 2 Acute Angles And Right Triangles 3 Radian Measure And The Unit Circle 4 Graphs Of The Circular Functions 5 Trigonometric Identities 6 Inverse Circular Functions And Trigonometric Equations 7 Applications Of Trigonometry And Vectors 8 Complex Numbers, Polar Equations, And Parametric Equations A Equations And Inequalities B Graphs Of Equations C Functions D Graphing Techniques Chapter1: Trigonometric Functions
1.1 Angles 1.2 Angle Relationships And Similar Triangles 1.3 Trigonometric Functions 1.4 Using The Definitions Of The Trigonometric Functions Chapter Questions Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Problem 2RE: Find the angle of least positive measure that is coterminal with each angle. 51 Problem 3RE:
Find the angle of least positive measure that is coterminal with each angle.
3. –174°
Problem 4RE: Find the angle of least positive measure that is coterminal with each angle. 792 Problem 5RE: Rotating Propeller The propeller of a speedboat rotates 650 times per min. Through how many degrees... Problem 6RE:
6. Rotating Pulley A pulley is rotating 320 times per min. Through how many degrees does a point on... Problem 7RE: Convert decimal degrees to degrees, minutes, seconds, and convert degrees, minutes, seconds to... Problem 8RE:
Convert decimal degrees to degrees, minutes, seconds, and convert degrees, minutes, seconds to... Problem 9RE:
Convert decimal degrees to degrees, minutes, seconds, and convert degrees, minutes, seconds to... Problem 10RE: Convert decimal degrees to degrees, minutes, seconds, and convert degrees, minutes, seconds to... Problem 11RE:
Find the measure of each marked angle.
11.
Problem 12RE: Find the measure of each marked angle. Problem 13RE Problem 14RE Problem 15RE: Length of a Road A camera is located on a satellite with its lens positioned at C in the figure.... Problem 16RE:
16. Express θ in terms of α and β
Problem 17RE: Find all unknown angle measures in each pair of similar triangles. Problem 18RE: Find all unknown angle measures in each pair of similar triangles. Problem 19RE:
Find the unknown side lengths in each pair of similar triangles.
19.
Problem 20RE Problem 21RE Problem 22RE Problem 23RE:
23. Length of a Shadow If a tree 20 ft tall casts a shadow 8 ft long, how long would the shadow of... Problem 24RE: Find the six trigonometric function values for each angle. Rationalize denominators when applicable. Problem 25RE Problem 26RE: Find the six trigonometric function values for each angle. Rationalize denominators when applicable. Problem 27RE Problem 28RE: Find the values of the six trigonometric functions for an angle in standard position having each... Problem 29RE Problem 30RE Problem 31RE Problem 32RE Problem 33RE: An equation of the terminal side of an angle θ in standard position is given with a restriction on... Problem 34RE: An equation of the terminal side of an angle in standard position is given with a restriction on x.... Problem 35RE:
An equation of the terminal side of an angle θ in standard position is given with a restriction on... Problem 36RE Problem 37RE Problem 38RE Problem 39RE:
Give all six trigonometric function values for each angle θ. Rationalize denominators when... Problem 40RE: Give all six trigonometric function values for each angle . Rationalize denominators when... Problem 41RE Problem 42RE Problem 43RE Problem 44RE:
Give all six trigonometric function values for each angle θ. Rationalize denominators when... Problem 45RE Problem 46RE: Concept Check If, for some particular angle , sin 0 and cos 0, in what quadrant must lie? What... Problem 47RE Problem 48RE Problem 49RE Problem 50RE: Height of a Lunar Peak The lunar mountain peak Huygens has a height of 21,000 ft. The shadow of... Problem 1T:
1. Give the measures of the complement and the supplement of an angle measuring 67°.
Problem 2T Problem 3T Problem 4T Problem 5T Problem 6T Problem 7T Problem 8T:
Perform each conversion.
8. 74° 18′ 36″ to decimal degrees
Problem 9T: Perform each conversion. 45.2025 to degrees, minutes, seconds Problem 10T: Solve each problem. Find the angle of least positive measure that is coterminal with each angle. (a)... Problem 11T Problem 12T Problem 13T Problem 14T:
Sketch an angle θ in standard position such that θ has the least positive measure, and the given... Problem 15T: Sketch an angle in standard position such that has the least positive measure, and the given point... Problem 16T Problem 17T: Complete the table with the appropriate function values of the given quadrantal angles. If the value... Problem 18T Problem 19T Problem 20T:
20. Decide whether each statement is possible or impossible.
(a) sin θ = 1.5 (b) sec θ = 4 (c) tan... Problem 21T: Find the value of sec if cos=712. Problem 22T: Find the five remaining trigonometric function values of if sin=37 and is in quadrant II. Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Concept explainers
Find the measure of angle α. Hint: Notice that this angle is the difference of the angle ADC and BDC.
Transcribed Image Text: The image depicts a geometric diagram with two right triangles sharing a common base \( CD \). The key features of the diagram are as follows:
- Triangle \( ABC \) is a right triangle with \( \angle ACB = 90^\circ \).
- The hypotenuse \( AB \) measures 16 units in length.
- Adjacent to angle \( A \), there is angle \( \theta \).
- \( BC \), the base of triangle \( ABC \), is perpendicular to \( AC \).
- Triangle \( BCD \) is another right triangle with \( \angle BCD = 90^\circ \).
- The length of \( CD \) is 10 units.
- Angle \( BDC \) measures \( 56^\circ \).
- Angle \( \alpha \) is adjacent to \( CD \).
The two triangles, \( ABC \) and \( BCD \), share the side \( BC \). The diagram may be used to explore relationships between the angles \( \theta \) and \( \alpha \), and to apply trigonometric identities or theorems to find unknown lengths or angles.
Figure in plane geometry formed by two rays or lines that share a common endpoint, called the vertex. The angle is measured in degrees using a protractor. The different types of angles are acute, obtuse, right, straight, and reflex.
Expert Solution
Step by step
Solved in 2 steps with 2 images