A 1.5 µF capacitor and a 4.2 µF capacitor are connected in parallel across a 240 V potential difference. Calculate the total energy in joules stored in the capacitors.
A 1.5 µF capacitor and a 4.2 µF capacitor are connected in parallel across a 240 V potential difference. Calculate the total energy in joules stored in the capacitors.
Related questions
Question
****Show all forces, motion/free-body diagrams, calculations, equations, significant figures and work. ****
![**Problem Statement:**
A 1.5 μF capacitor and a 4.2 μF capacitor are connected in parallel across a 240 V potential difference. Calculate the total energy in joules stored in the capacitors.
**Explanation:**
When capacitors are connected in parallel, the total capacitance (C_total) is the sum of the individual capacitances:
\[ C_{\text{total}} = C_1 + C_2 \]
Given:
- \( C_1 = 1.5 \, \mu \text{F} = 1.5 \times 10^{-6} \, \text{F} \)
- \( C_2 = 4.2 \, \mu \text{F} = 4.2 \times 10^{-6} \, \text{F} \)
- Voltage (V) = 240 V
First, calculate the total capacitance:
\[ C_{\text{total}} = 1.5 \times 10^{-6} + 4.2 \times 10^{-6} = 5.7 \times 10^{-6} \, \text{F} \]
The energy \( E \) stored in a capacitor is given by the formula:
\[ E = \frac{1}{2} C V^2 \]
Substitute the total capacitance and voltage into the formula to find the energy:
\[ E = \frac{1}{2} \times 5.7 \times 10^{-6} \times (240)^2 \]
Calculate:
\[ E = \frac{1}{2} \times 5.7 \times 10^{-6} \times 57600 \]
\[ E = 0.163944 \, \text{J} \]
Therefore, the total energy stored in the capacitors is approximately 0.164 joules.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F8669c346-3c1c-4fba-9bd7-ca273b01942a%2Fb458ea97-f89a-4e41-8806-0673a955bfc4%2Fpk1gkdk_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
A 1.5 μF capacitor and a 4.2 μF capacitor are connected in parallel across a 240 V potential difference. Calculate the total energy in joules stored in the capacitors.
**Explanation:**
When capacitors are connected in parallel, the total capacitance (C_total) is the sum of the individual capacitances:
\[ C_{\text{total}} = C_1 + C_2 \]
Given:
- \( C_1 = 1.5 \, \mu \text{F} = 1.5 \times 10^{-6} \, \text{F} \)
- \( C_2 = 4.2 \, \mu \text{F} = 4.2 \times 10^{-6} \, \text{F} \)
- Voltage (V) = 240 V
First, calculate the total capacitance:
\[ C_{\text{total}} = 1.5 \times 10^{-6} + 4.2 \times 10^{-6} = 5.7 \times 10^{-6} \, \text{F} \]
The energy \( E \) stored in a capacitor is given by the formula:
\[ E = \frac{1}{2} C V^2 \]
Substitute the total capacitance and voltage into the formula to find the energy:
\[ E = \frac{1}{2} \times 5.7 \times 10^{-6} \times (240)^2 \]
Calculate:
\[ E = \frac{1}{2} \times 5.7 \times 10^{-6} \times 57600 \]
\[ E = 0.163944 \, \text{J} \]
Therefore, the total energy stored in the capacitors is approximately 0.164 joules.
Expert Solution
Step 1
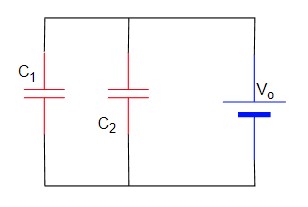
Given that,
the capacitance of the two capacitors which are connected in parallel are
And the applied voltage is
Step by step
Solved in 3 steps with 1 images
