A 1-kg mass is attached to a spring with stiffness 1 N/m. The damping constant for the suystem is 2 N-sec/m. At time t=0, the mass is compressed 20 cm (=0.2 m) to the left and given an initial velocity of 30 cm/sec (=0.3 m/sec) to the right. (a) The position x(t) of the mass at time t is given by OA. sint -2 cos t 10 O B. O C. O D. x(t) = x(t)= x(t) = 2-1 10 t-2 10 et -t 4√3 sin √3t 2 -t e - 6 cos x(t) = 30 OE. None of the given answer √3t 2 ect
A 1-kg mass is attached to a spring with stiffness 1 N/m. The damping constant for the suystem is 2 N-sec/m. At time t=0, the mass is compressed 20 cm (=0.2 m) to the left and given an initial velocity of 30 cm/sec (=0.3 m/sec) to the right. (a) The position x(t) of the mass at time t is given by OA. sint -2 cos t 10 O B. O C. O D. x(t) = x(t)= x(t) = 2-1 10 t-2 10 et -t 4√3 sin √3t 2 -t e - 6 cos x(t) = 30 OE. None of the given answer √3t 2 ect
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Part a

Transcribed Image Text:The text describes a physics problem related to a damped harmonic oscillator system:
---
A 1-kg mass is attached to a spring with a stiffness of 1 N/m. The damping constant for the system is 2 N-sec/m. At time \( t = 0 \), the mass is compressed 20 cm (0.2 m) to the left and given an initial velocity of 30 cm/sec (0.3 m/sec) to the right.
(a) The position \( x(t) \) of the mass at time \( t \) is given by:
- **A.** \( x(t) = \frac{{\sin t - 2 \cos t}}{10} e^{-t} \)
- **B.** \( x(t) = \frac{{2 - t}}{10} e^{t} \)
- **C.** \( x(t) = \frac{{t - 2}}{10} e^{-t} \)
- **D.** \( x(t) = \frac{{4 \sqrt{3} \sin \frac{\sqrt{3} t}{2} - 6 \cos \frac{\sqrt{3} t}{2}}}{30} e^{-\frac{t}{2}} \)
- **E.** None of the given answers are correct
---
No graphs or diagrams are present in the image. The problem involves selecting the correct formula for the position of the mass as a function of time, considering the given conditions of an initial compression and velocity, with a specified damping constant.
Expert Solution
Step 1
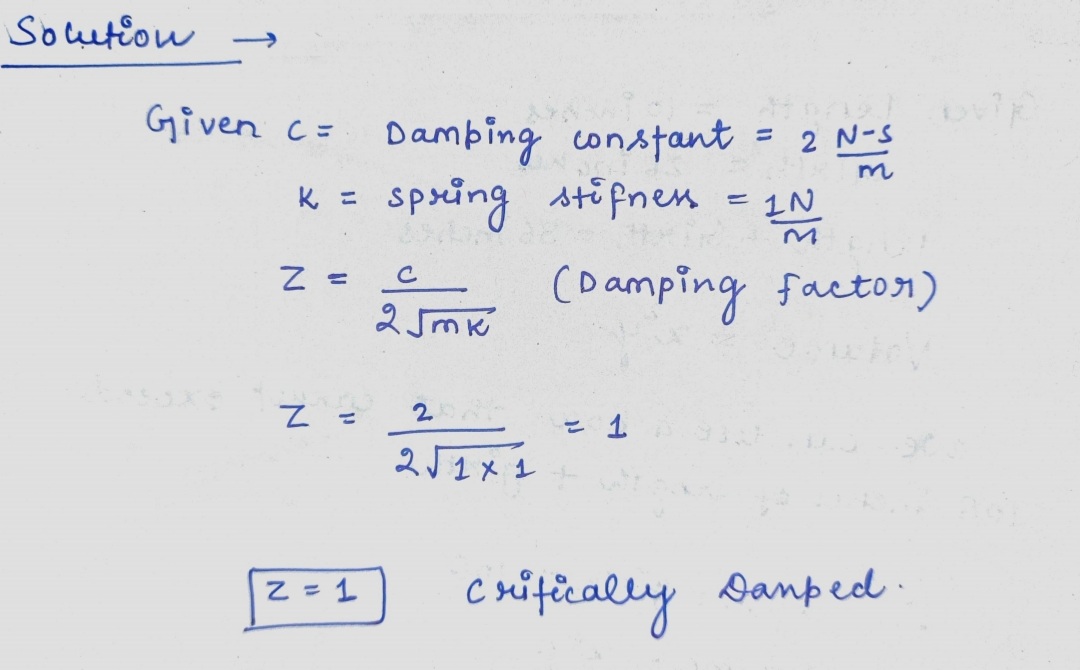
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

