9) For the 2p, orbital, what is the most probable point (r, 8, d) where an e- will be found. R₁, Y₁ = fi ce -$12 3 2,1 1,0 √24 a. pe 3/2 "pe²³ ) ² = 0 d Z dx √24 a. pe 4T COSO 2 (COSO )² = 0
9) For the 2p, orbital, what is the most probable point (r, 8, d) where an e- will be found. R₁, Y₁ = fi ce -$12 3 2,1 1,0 √24 a. pe 3/2 "pe²³ ) ² = 0 d Z dx √24 a. pe 4T COSO 2 (COSO )² = 0
Chemistry
10th Edition
ISBN:9781305957404
Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Chapter1: Chemical Foundations
Section: Chapter Questions
Problem 1RQ: Define and explain the differences between the following terms. a. law and theory b. theory and...
Related questions
Question
![**Question 9: For the 2p\(_z\) orbital, what is the most probable point \((r, \theta, \phi)\) where an electron will be found?**
The expression for the radial and angular parts is:
\[
R_{2,1}Y_{1,0} = \left(\frac{1}{\sqrt{24}}\right)\left(\frac{z}{a_0}\right)^{3/2} pe^{-r/2}\sqrt{\frac{3}{4\pi}} \cos\theta
\]
To find the most probable point, the first derivative of the probability density with respect to the position \(x\) is set to zero:
\[
\frac{d}{dx} \left(\sqrt{\frac{3}{4\pi}} \cos\theta \right)^2 = 0
\]
And:
\[
\frac{d}{dx} \left(\frac{1}{\sqrt{24}}\left(\frac{z}{a_0}\right)^{3/2} pe^{-r/2} \right)^2 = 0
\]
This involves determining where the derivative of the probability density function is zero, indicating points of maximum probability.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F1fed7a52-65d8-44f4-988f-6c762cda0c09%2F7c937233-99ad-402e-aa8f-d8c463d55a3b%2Fd0rzhfp_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Question 9: For the 2p\(_z\) orbital, what is the most probable point \((r, \theta, \phi)\) where an electron will be found?**
The expression for the radial and angular parts is:
\[
R_{2,1}Y_{1,0} = \left(\frac{1}{\sqrt{24}}\right)\left(\frac{z}{a_0}\right)^{3/2} pe^{-r/2}\sqrt{\frac{3}{4\pi}} \cos\theta
\]
To find the most probable point, the first derivative of the probability density with respect to the position \(x\) is set to zero:
\[
\frac{d}{dx} \left(\sqrt{\frac{3}{4\pi}} \cos\theta \right)^2 = 0
\]
And:
\[
\frac{d}{dx} \left(\frac{1}{\sqrt{24}}\left(\frac{z}{a_0}\right)^{3/2} pe^{-r/2} \right)^2 = 0
\]
This involves determining where the derivative of the probability density function is zero, indicating points of maximum probability.
Expert Solution
Step 1
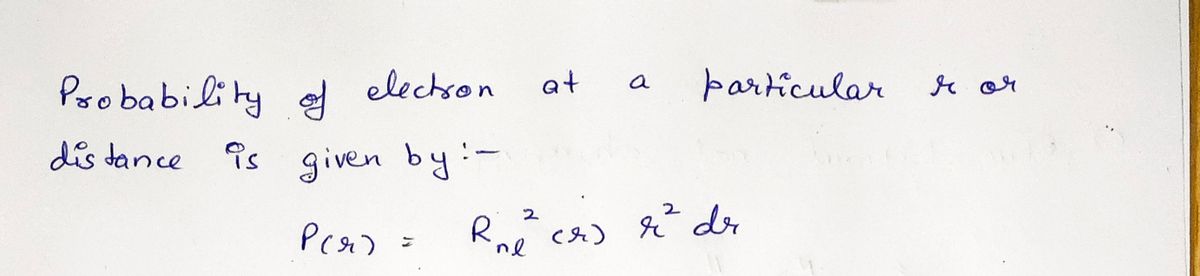
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, chemistry and related others by exploring similar questions and additional content below.Recommended textbooks for you

Chemistry
Chemistry
ISBN:
9781305957404
Author:
Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher:
Cengage Learning

Chemistry
Chemistry
ISBN:
9781259911156
Author:
Raymond Chang Dr., Jason Overby Professor
Publisher:
McGraw-Hill Education

Principles of Instrumental Analysis
Chemistry
ISBN:
9781305577213
Author:
Douglas A. Skoog, F. James Holler, Stanley R. Crouch
Publisher:
Cengage Learning

Chemistry
Chemistry
ISBN:
9781305957404
Author:
Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher:
Cengage Learning

Chemistry
Chemistry
ISBN:
9781259911156
Author:
Raymond Chang Dr., Jason Overby Professor
Publisher:
McGraw-Hill Education

Principles of Instrumental Analysis
Chemistry
ISBN:
9781305577213
Author:
Douglas A. Skoog, F. James Holler, Stanley R. Crouch
Publisher:
Cengage Learning

Organic Chemistry
Chemistry
ISBN:
9780078021558
Author:
Janice Gorzynski Smith Dr.
Publisher:
McGraw-Hill Education

Chemistry: Principles and Reactions
Chemistry
ISBN:
9781305079373
Author:
William L. Masterton, Cecile N. Hurley
Publisher:
Cengage Learning

Elementary Principles of Chemical Processes, Bind…
Chemistry
ISBN:
9781118431221
Author:
Richard M. Felder, Ronald W. Rousseau, Lisa G. Bullard
Publisher:
WILEY