8. We defined the standard order and the divisibility order | for natural numbers from the operations + (whose identity is 0) and (whose identity is 1), respectively, using very similar definitions and proved that they satisfied similar properties. We can do it in a more abstract setting following exactly the same ideas: Suppose that we are given a set X together with an operation * on X and a particular element e E X satisfying the following properties: the operation is associative: that is, for all a, b, c E X, we have a* (b* c) = (a*b) * c. e is an identity for *: that is, for every a E X, a *e = a and e* a = a. Se define the relation as follows: for all a, b E X, we have that ab if and only if a* d = b for some d E X.
8. We defined the standard order and the divisibility order | for natural numbers from the operations + (whose identity is 0) and (whose identity is 1), respectively, using very similar definitions and proved that they satisfied similar properties. We can do it in a more abstract setting following exactly the same ideas: Suppose that we are given a set X together with an operation * on X and a particular element e E X satisfying the following properties: the operation is associative: that is, for all a, b, c E X, we have a* (b* c) = (a*b) * c. e is an identity for *: that is, for every a E X, a *e = a and e* a = a. Se define the relation as follows: for all a, b E X, we have that ab if and only if a* d = b for some d E X.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
(a) Prove that ⊑ is transitive, that is, we have that if a V b and b ⊑ c, then a ⊑ c.
(b) Prove that ⊑ is anti-symmetric, that is, we have that if a ⊑ b and ⊑ a, then a = b
- for all x, y ∈ X, if x*y=e then x = e
- for all x, y, z ∈ X, if x*y=x*z hen y = z

Transcribed Image Text:8. We defined the standard order and the divisibility order | for natural numbers from the operations
+ (whose identity is 0) and (whose identity is 1), respectively, using very similar definitions and proved
that they satisfied similar properties. We can do it in a more abstract setting following exactly the
same ideas: Suppose that we are given a set X together with an operation * on X and a particular
element e E X satisfying the following properties:
• the operation is associative: that is, for all a, b, c E X, we have a * (b* c) = (a*b) * c.
e is an identity for *: that is, for every a E X, a* e = a and e* a = a.
Se define the relation as follows: for all a, b E X, we have that
ab if and only if
a* d = b for some de X.
Expert Solution
Step 1
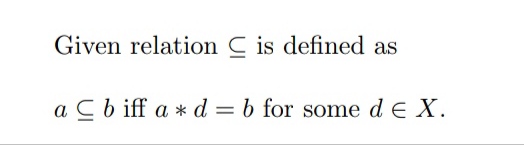
Step by step
Solved in 3 steps with 3 images

Similar questions
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

