Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
#19 can you help me with this? I’ve attached my work.
![**Problem Statement:**
Evaluate the limit, if it exists. (If an answer does not exist, enter DNE.)
\[
\lim_{{t \to 0}} \left( \frac{8}{t} - \frac{8}{t^2 + t} \right)
\]
**Solution Submitted:**
- Answer given: "dne"
- Marked as incorrect.
**Help Resources:**
- Button labeled "Watch It" for additional assistance.
- Section titled "Additional Materials" with a link to an "eBook" for further reading.
---
To solve the problem, consider simplifying the expression and using techniques like factoring or L'Hôpital's rule, if applicable.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F5f440a4a-a87c-43e8-9c30-e4890b6a6760%2F6ee6b9a8-a388-4b05-a187-c5f432a44d2e%2Fdmrxmv_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Evaluate the limit, if it exists. (If an answer does not exist, enter DNE.)
\[
\lim_{{t \to 0}} \left( \frac{8}{t} - \frac{8}{t^2 + t} \right)
\]
**Solution Submitted:**
- Answer given: "dne"
- Marked as incorrect.
**Help Resources:**
- Button labeled "Watch It" for additional assistance.
- Section titled "Additional Materials" with a link to an "eBook" for further reading.
---
To solve the problem, consider simplifying the expression and using techniques like factoring or L'Hôpital's rule, if applicable.
![Below is a transcription of the handwritten mathematical work on the page:
---
The work appears to involve evaluating a limit:
1. Start with the expression:
\[
\lim_{{x \to 6}} \frac{{8 - (8x / (x+2) + 5)}}{{x - 6}}
\]
2. Begin simplifying the numerator:
\[
8 - \left( \frac{{8x}}{{x+2}} + 5 \right) = \frac{{8(x+2)}}{{x+2}} - \frac{{8x}}{{x+2}} - \frac{{5(x+2)}}{{x+2}}
\]
3. Simplifying further, combine the fractions:
\[
\frac{{8x + 16 - 8x - 5x - 10}}{{x+2}} = \frac{{3x + 6}}{{x+2}}
\]
4. Substitute into the overall expression:
\[
\lim_{{x \to 6}} \frac{{(3x + 6)/(x+2)}}{{x - 6}}
\]
5. Simplify and evaluate the limit:
\[
\lim_{{x \to 6}} \frac{{3x + 6}}{{(x+2)(x-6)}}
\]
This expression needs further factorization or approaches, such as using L'Hôpital's Rule if an indeterminate form like \(0/0\) is present when \(x = 6\). Alternatively, recognition of a common factor in the numerator and the denominator might allow for simpler evaluation.
**No graphs or diagrams are present in this transcription.**
---](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F5f440a4a-a87c-43e8-9c30-e4890b6a6760%2F6ee6b9a8-a388-4b05-a187-c5f432a44d2e%2Fnjrugkk_processed.jpeg&w=3840&q=75)
Transcribed Image Text:Below is a transcription of the handwritten mathematical work on the page:
---
The work appears to involve evaluating a limit:
1. Start with the expression:
\[
\lim_{{x \to 6}} \frac{{8 - (8x / (x+2) + 5)}}{{x - 6}}
\]
2. Begin simplifying the numerator:
\[
8 - \left( \frac{{8x}}{{x+2}} + 5 \right) = \frac{{8(x+2)}}{{x+2}} - \frac{{8x}}{{x+2}} - \frac{{5(x+2)}}{{x+2}}
\]
3. Simplifying further, combine the fractions:
\[
\frac{{8x + 16 - 8x - 5x - 10}}{{x+2}} = \frac{{3x + 6}}{{x+2}}
\]
4. Substitute into the overall expression:
\[
\lim_{{x \to 6}} \frac{{(3x + 6)/(x+2)}}{{x - 6}}
\]
5. Simplify and evaluate the limit:
\[
\lim_{{x \to 6}} \frac{{3x + 6}}{{(x+2)(x-6)}}
\]
This expression needs further factorization or approaches, such as using L'Hôpital's Rule if an indeterminate form like \(0/0\) is present when \(x = 6\). Alternatively, recognition of a common factor in the numerator and the denominator might allow for simpler evaluation.
**No graphs or diagrams are present in this transcription.**
---
Expert Solution
Basic
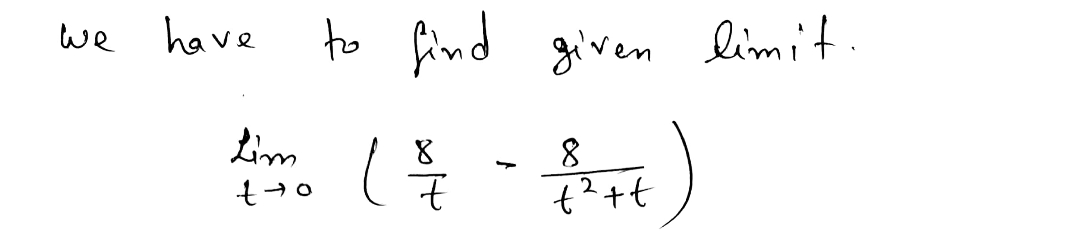
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning