θ = cos^-1[sin(LT1) sin(LT2) + cos(LT1) cos(LT2) cos(LN1 − LN2)] How does this formula go with latitude and longitude corrdinates?
θ = cos^-1[sin(LT1) sin(LT2) + cos(LT1) cos(LT2) cos(LN1 − LN2)]
How does this formula go with latitude and longitude corrdinates?
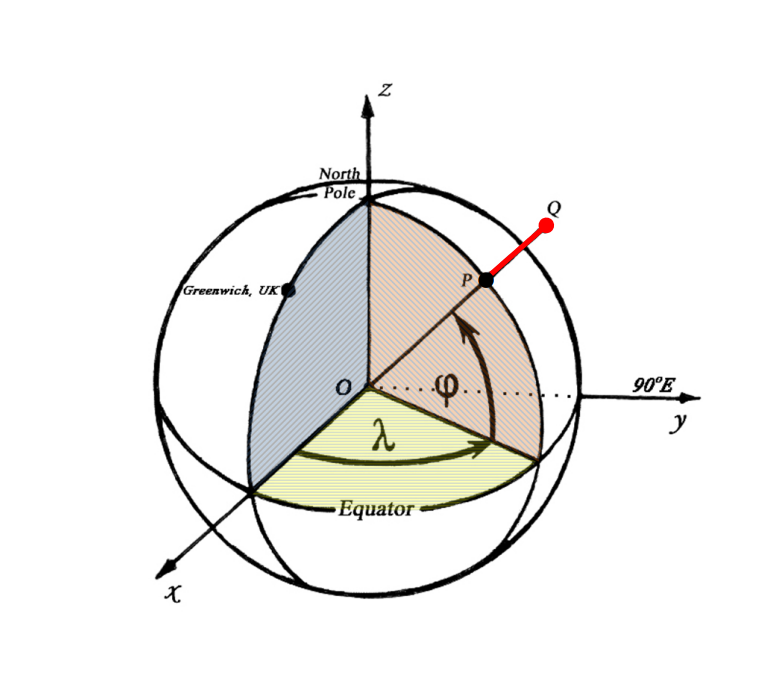
Consider the figure as our Earth.
is the center of the earth
Point on the earth surface has Latitude and Longitude
In general we take :
where is the radius of the Earth
With respect to the Cartesian co-ordinates axes: and we have
If Distance from to the center of the earth in the figure above, then
the straight line , linear distance between any two point and in space may be computed from their Cartesian Coordinates.
If and then
If is the angle formed between any two points and on the surface of the Earth with , the center of the Earth, then
In the above formula , assume has (Longitude Longitude)
and has (Longitude Longitude)
The geodesic or surface distance, , between the points and measured along a great circle of the Earth is
where
Step by step
Solved in 2 steps with 2 images









