Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
8 -6 -4 2 0 --2- (1,0) Graph of f(x) -~ 2 (3, 0)

8 -6 -4 2 0 --2- (1,0) Graph of f(x) -~ 2 (3, 0)

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
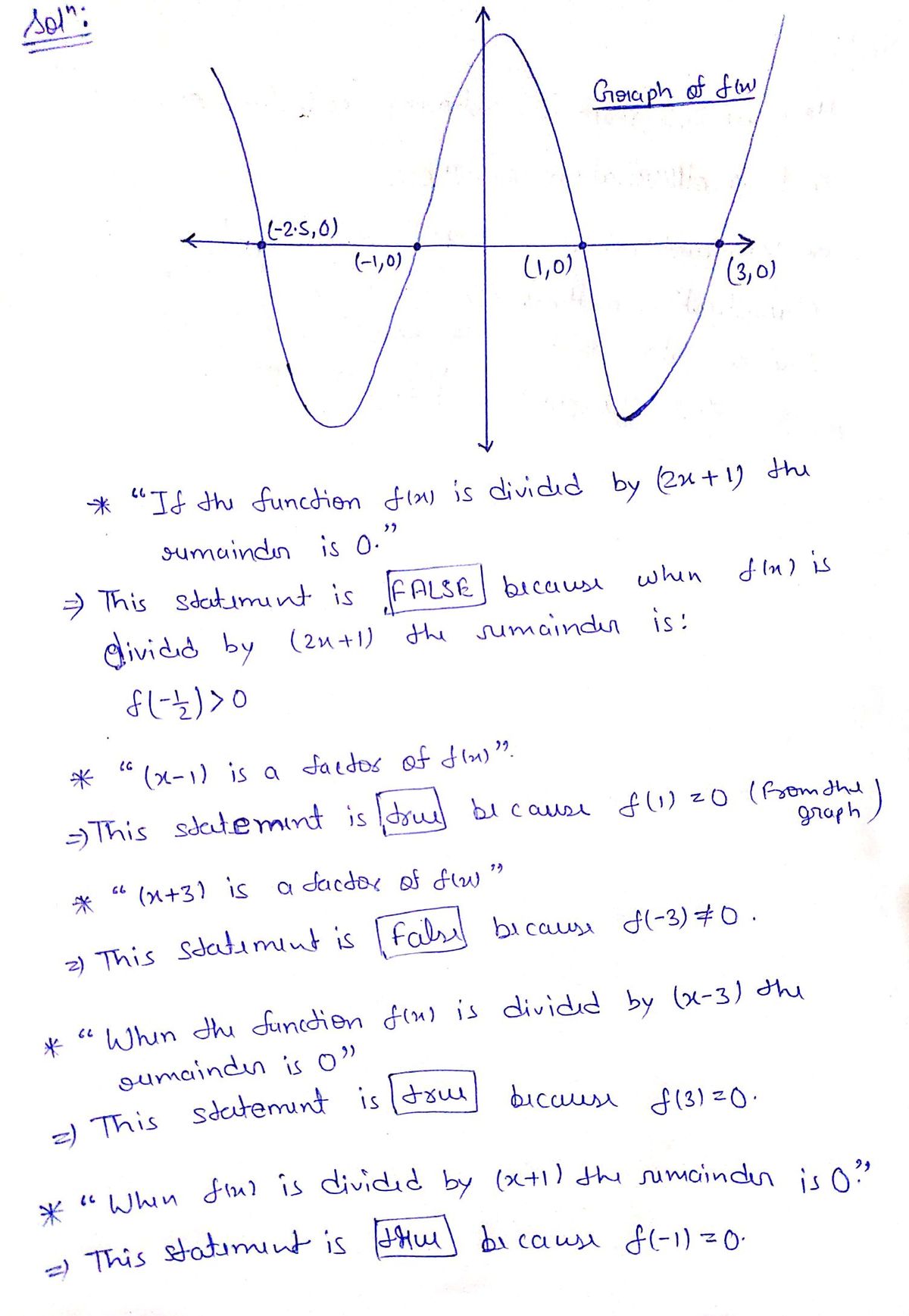
### Graph Details The image displays the graph of a polynomial function \( f(x) \). The graph intersects the x-axis at three points: \( (-2.5, 0) \), \( (-1, 0) \), and \( (3, 0) \). These points are the roots of the polynomial. ### Questions and Options: Given the graph of the polynomial function \( f(x) \) above, which of the following statements must be true? Select all that apply. - [ ] If the function \( f(x) \) is divided by \( (2x+1) \) the remainder is 0 - [ ] \( (x-1) \) is a factor of \( f(x) \) - [ ] \( (x+3) \) is a factor of \( f(x) \) - [ ] When the function \( f(x) \) is divided by \( (x-3) \) the remainder is 0 - [ ] When \( f(x) \) is divided by \( (x+1) \) the remainder is 0 ### Explanation On an educational website, it is essential to analyze the roots of the polynomial based on where it crosses the x-axis. Each root corresponds to a factor of the polynomial: - The root at \( x = -2.5 \) suggests a factor can be derived, but it does not match any integer-based factor from standard polynomials. - The roots at \( x = -1 \) and \( x = 3 \) suggest the polynomial can be factored to include \( (x + 1) \) and \( (x - 3) \), respectively. Thus, statements involving these factors might apply.
Transcribed Image Text:### Graph Details The image displays the graph of a polynomial function \( f(x) \). The graph intersects the x-axis at three points: \( (-2.5, 0) \), \( (-1, 0) \), and \( (3, 0) \). These points are the roots of the polynomial. ### Questions and Options: Given the graph of the polynomial function \( f(x) \) above, which of the following statements must be true? Select all that apply. - [ ] If the function \( f(x) \) is divided by \( (2x+1) \) the remainder is 0 - [ ] \( (x-1) \) is a factor of \( f(x) \) - [ ] \( (x+3) \) is a factor of \( f(x) \) - [ ] When the function \( f(x) \) is divided by \( (x-3) \) the remainder is 0 - [ ] When \( f(x) \) is divided by \( (x+1) \) the remainder is 0 ### Explanation On an educational website, it is essential to analyze the roots of the polynomial based on where it crosses the x-axis. Each root corresponds to a factor of the polynomial: - The root at \( x = -2.5 \) suggests a factor can be derived, but it does not match any integer-based factor from standard polynomials. - The roots at \( x = -1 \) and \( x = 3 \) suggest the polynomial can be factored to include \( (x + 1) \) and \( (x - 3) \), respectively. Thus, statements involving these factors might apply.
Expert Solution
Step 1

Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 1 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS