**Exercise: Verifying Probability Distributions**In this exercise, you are tasked to verify the given table as a probability distribution. You will need to draw a graph to represent the data visually, and then calculate the mean, variance, and standard deviation of this distribution.**Table: Probability Distribution**| x | P(x) ||----|------|| 2 | 0.52 || 4 | 0.12 || 6 | 0.28 || 8 | 0.08 |This table lists values of a random variable $ x $ and their corresponding probabilities $ P(x) $. Ensure that the sum of all probabilities equals 1 to confirm it's a valid probability distribution.**Steps to Follow:**1. **Check Probability Sum:** Verify that the sum of $ P(x) $ values is 1.2. **Graph the Data:** Create a bar graph or histogram to represent the distribution visually.3. **Calculate Mean ($\mu$)**: Use the formula $\mu = \sum (x \cdot P(x))$.4. **Calculate Variance ($\sigma^2$)**: Use the formula $\sigma^2 = \sum ((x - \mu)^2 \cdot P(x))$.5. **Calculate Standard Deviation ($\sigma$)**: This is the square root of the variance, $\sigma = \sqrt{\sigma^2}$.Through this exercise, you will gain hands-on experience in handling basic probability distributions and performing related statistical calculations.

Answered: 7. Verify the following table as a…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Concept explainers

Question

**Exercise: Verifying Probability Distributions**

In this exercise, you are tasked to verify the given table as a probability distribution. You will need to draw a graph to represent the data visually, and then calculate the mean, variance, and standard deviation of this distribution.

**Table: Probability Distribution**

| x | P(x) |
|----|------|
| 2 | 0.52 |
| 4 | 0.12 |
| 6 | 0.28 |
| 8 | 0.08 |

This table lists values of a random variable $ x $ and their corresponding probabilities $ P(x) $. Ensure that the sum of all probabilities equals 1 to confirm it's a valid probability distribution.

**Steps to Follow:**

1. **Check Probability Sum:** Verify that the sum of $ P(x) $ values is 1.
2. **Graph the Data:** Create a bar graph or histogram to represent the distribution visually.
3. **Calculate Mean ($\mu$)**: Use the formula $\mu = \sum (x \cdot P(x))$.
4. **Calculate Variance ($\sigma^2$)**: Use the formula $\sigma^2 = \sum ((x - \mu)^2 \cdot P(x))$.
5. **Calculate Standard Deviation ($\sigma$)**: This is the square root of the variance, $\sigma = \sqrt{\sigma^2}$.

Through this exercise, you will gain hands-on experience in handling basic probability distributions and performing related statistical calculations.

Expert Solution

Step 1

Conditions for discrete probability distribution:

The following requirements should be satisfied for the distribution to follow discrete probability distribution.

The given random variable (X) must take up finite or countable values and it should have its corresponding probabilities.
The sum of all probabilities must be equal to 1. That is, ∑P(X)=1.
The probability values must lie between 0 and 1, inclusive. That is, 0≤ P(X)≤1.

Here, the random variable X takes values, 2, 4,6 and 8. Hence the first condition is satisfied.

Consider, ∑P(X)=1. Now, ∑P(X)= 0.52+0.12+0.28+0.08 =1. Hence the second condition is satisfied.

Also, all probability values lie between 0 and 1. Thus, the third condition is satisfied.

Thus, the table represents a probability distribution.

Step 2

The required calculations for obtaining mean, variance and standard deviation are made in the following table:

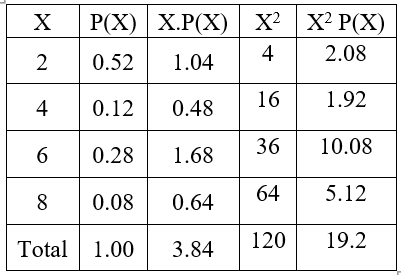
The expected value is calculated as follows:

μ= $\sum_{}$ XP(X)

= 3.84

The mean is 3.84.

The variance is calculated as follows:

Variance=∑X²P(X)-E(X)²

=19.2-(3.84)²

=4.4544

Thus, the variance is 4.4544.

Standard deviation = $\sqrt{}$ variance = $\sqrt{}$ 4.4544 = 2.11.

The standard deviation is 2.11.

Trending now

This is a popular solution!

Step by step

Solved in 3 steps with 2 images

Knowledge Booster

$Point Estimation, Limit Theorems, Approximations, and Bounds$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions