7. Establish for A is m × n and B, C are n x p, that A(B+C) = AB + AC
Algebra for College Students
10th Edition
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Jerome E. Kaufmann, Karen L. Schwitters
Chapter12: Algebra Of Matrices
Section12.1: Algebra Of 2 X 2 Matrices
Problem 45PS
Related questions
Question

Transcribed Image Text:### Problem Statement
7. Establish for \( A \) is \( m \times n \) and \( B, C \) are \( n \times p \), that \( A(B + C) = AB + AC \).
---
This problem requires you to demonstrate the distributive property of matrix multiplication. You must show that multiplying a matrix \( A \) by the sum of two matrices \( B \) and \( C \) results in the same matrix as multiplying \( A \) by \( B \) and \( A \) by \( C \) separately, and then adding the results.
**Explanation:**
- **Matrix Dimensions:**
- \( A \) is an \( m \times n \) matrix.
- \( B \) and \( C \) are both \( n \times p \) matrices.
- **Operation:**
- \( A(B + C) \) means that you first perform the matrix addition \( B + C \), which is defined because \( B \) and \( C \) have the same dimensions, and then multiply the resulting matrix by \( A \).
- The result will be an \( m \times p \) matrix.
- **Distributive Property:**
- You need to show that this operation is the same as calculating \( AB \) and \( AC \) (which are also \( m \times p \) matrices) and then adding them together.
This property is a fundamental aspect of matrix algebra and is used extensively in various applications involving linear transformations and systems of equations.
Expert Solution
Step 1
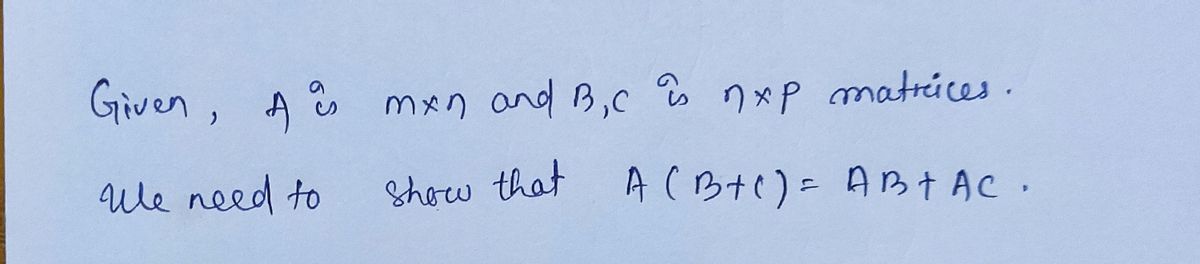
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Algebra for College Students
Algebra
ISBN:
9781285195780
Author:
Jerome E. Kaufmann, Karen L. Schwitters
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning


Algebra for College Students
Algebra
ISBN:
9781285195780
Author:
Jerome E. Kaufmann, Karen L. Schwitters
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning



College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning