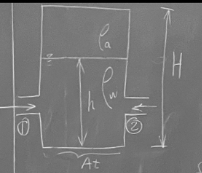
7 At Find the expression for. dh at Of 2 Compute att if D₁ = 1. in dh T=2=C D₂ = 3 in V₁ = 3 ft/ V2=24% 4 T₁ At = 2 ft²
7 At Find the expression for. dh at Of 2 Compute att if D₁ = 1. in dh T=2=C D₂ = 3 in V₁ = 3 ft/ V2=24% 4 T₁ At = 2 ft²
Elements Of Electromagnetics
7th Edition
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Sadiku, Matthew N. O.
ChapterMA: Math Assessment
Section: Chapter Questions
Problem 1.1MA
Related questions
Topic Video
Question
Please, I want step-by-step solution 
![### Fluid Mechanics Chalkboard Notes
#### Diagram Explanation:
A schematic with a rectangular section indicates a control volume in fluid mechanics where:
- \( \rho_a \) is the air density
- \( \rho_w \) is the water density
- \( H \) is the total height
- \( h \) is the height of the water within the control volume
- Dimensions are annotated, indicating 2 points where fluid enters and exits.
#### Mathematical Derivations:
1. **Expression Derivation:**
- Task to find the expression for \( \frac{dh}{dt} \), the rate of change of height with respect to time.
2. **Calculation Example:**
- Compute \( \frac{dh}{dt} \) given:
- \( D_1 = 1\) in (Diameter 1)
- \( D_2 = 3\) in (Diameter 2)
- \( V_1 = 3\) ft/s (Velocity 1)
- \( V_2 = 2\) ft/s (Velocity 2)
- \( A_t = 2\) ft\(^2\) (Area)
- Temperature \( T = 20^\circ C \)
#### Equations:
- **Cross-Sectional Area:**
\[
A = \frac{\pi}{4}D^2
\]
- **Volume Flow Rate Change:**
\[
O = \frac{d}{dt} \int_{cv} \rho dV - \rho_1 A_1 V_1 - \rho_2 A_2 V_1
\]
- **Continuity Equation:**
\[
\frac{d}{dt} \left( \int_{cv} \rho dV \right) = \frac{d}{dt}(\rho_w A_t h) + \frac{d}{dt}(\rho A_t (H - h))
\]
- **Simplified Form:**
\[
\frac{d}{dt}(\rho_w A_t h) = \rho_1 A_1 V_1 + \rho_2 A_2 V_2
\]
These notes illustrate the application of the continuity equation and the derivation of related variables in fluid mechanics, with specific inputs given for practice calculations.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F4ce8b870-93ef-497a-8c2a-bbbd1041dd5b%2Fe5b58bc5-71bc-418b-8314-73ae2b6a8a87%2F9g6a7jp_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Fluid Mechanics Chalkboard Notes
#### Diagram Explanation:
A schematic with a rectangular section indicates a control volume in fluid mechanics where:
- \( \rho_a \) is the air density
- \( \rho_w \) is the water density
- \( H \) is the total height
- \( h \) is the height of the water within the control volume
- Dimensions are annotated, indicating 2 points where fluid enters and exits.
#### Mathematical Derivations:
1. **Expression Derivation:**
- Task to find the expression for \( \frac{dh}{dt} \), the rate of change of height with respect to time.
2. **Calculation Example:**
- Compute \( \frac{dh}{dt} \) given:
- \( D_1 = 1\) in (Diameter 1)
- \( D_2 = 3\) in (Diameter 2)
- \( V_1 = 3\) ft/s (Velocity 1)
- \( V_2 = 2\) ft/s (Velocity 2)
- \( A_t = 2\) ft\(^2\) (Area)
- Temperature \( T = 20^\circ C \)
#### Equations:
- **Cross-Sectional Area:**
\[
A = \frac{\pi}{4}D^2
\]
- **Volume Flow Rate Change:**
\[
O = \frac{d}{dt} \int_{cv} \rho dV - \rho_1 A_1 V_1 - \rho_2 A_2 V_1
\]
- **Continuity Equation:**
\[
\frac{d}{dt} \left( \int_{cv} \rho dV \right) = \frac{d}{dt}(\rho_w A_t h) + \frac{d}{dt}(\rho A_t (H - h))
\]
- **Simplified Form:**
\[
\frac{d}{dt}(\rho_w A_t h) = \rho_1 A_1 V_1 + \rho_2 A_2 V_2
\]
These notes illustrate the application of the continuity equation and the derivation of related variables in fluid mechanics, with specific inputs given for practice calculations.
![The chalkboard contains a series of equations and a labeled diagram related to fluid dynamics. The content appears to be an analysis involving the continuity equation and fluid flow through a control volume.
### Diagram:
- A vertical container with variable dimensions is depicted.
- Height is labeled as \( H \).
- Different sections of the container are shown, each with certain flow parameters.
### Equations:
1. **Conservation of Mass/Continuity Equation:**
\[
O = \frac{d}{dt} \int_{cv} \rho dV = -\rho_1 A_1 V_1 - \rho_2 A_2 V_2
\]
2. **Time Rate of Change of Mass:**
\[
\frac{d}{dt} \int_{cv} \rho dV = \frac{d}{dt} (\rho_w A_t h) + \ldots
\]
3. **Expression Relating Change in Height:**
\[
\frac{d}{dt} (\rho_w A_t h) = \rho_1 A_1 V_1 + \rho_2 A_2 V_2
\]
4. **Derivation of Height Change Expression:**
\[
\rho(A_t) \frac{dh}{dt} = \rho(A_1 V_1 + A_2 V_2)
\]
5. **Simplified Equation of Height Change:**
\[
\frac{dh}{dt} = \frac{A_1 V_1 + A_2 V_2}{A_t}
\]
### Given Parameters:
- Diameter \( D_1 = 1 \) inch
- Diameter \( D_2 = 3 \) inches
- Velocity \( V_1 = 3 \) ft/s
- Velocity \( V_2 = 2 \) ft/s
- Total Area \( A_t = 2 \) ft²
This educational content serves to explain fluid flow and mass conservation principles in a control volume context, particularly illustrating the impact of varying flow rates and dimensions on fluid height within a system.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F4ce8b870-93ef-497a-8c2a-bbbd1041dd5b%2Fe5b58bc5-71bc-418b-8314-73ae2b6a8a87%2F5qytw2a_processed.jpeg&w=3840&q=75)
Transcribed Image Text:The chalkboard contains a series of equations and a labeled diagram related to fluid dynamics. The content appears to be an analysis involving the continuity equation and fluid flow through a control volume.
### Diagram:
- A vertical container with variable dimensions is depicted.
- Height is labeled as \( H \).
- Different sections of the container are shown, each with certain flow parameters.
### Equations:
1. **Conservation of Mass/Continuity Equation:**
\[
O = \frac{d}{dt} \int_{cv} \rho dV = -\rho_1 A_1 V_1 - \rho_2 A_2 V_2
\]
2. **Time Rate of Change of Mass:**
\[
\frac{d}{dt} \int_{cv} \rho dV = \frac{d}{dt} (\rho_w A_t h) + \ldots
\]
3. **Expression Relating Change in Height:**
\[
\frac{d}{dt} (\rho_w A_t h) = \rho_1 A_1 V_1 + \rho_2 A_2 V_2
\]
4. **Derivation of Height Change Expression:**
\[
\rho(A_t) \frac{dh}{dt} = \rho(A_1 V_1 + A_2 V_2)
\]
5. **Simplified Equation of Height Change:**
\[
\frac{dh}{dt} = \frac{A_1 V_1 + A_2 V_2}{A_t}
\]
### Given Parameters:
- Diameter \( D_1 = 1 \) inch
- Diameter \( D_2 = 3 \) inches
- Velocity \( V_1 = 3 \) ft/s
- Velocity \( V_2 = 2 \) ft/s
- Total Area \( A_t = 2 \) ft²
This educational content serves to explain fluid flow and mass conservation principles in a control volume context, particularly illustrating the impact of varying flow rates and dimensions on fluid height within a system.
Expert Solution
Step 1: Write the given data and what is to find
Given:
To find:
Find an expression for the change in water height.
Step by step
Solved in 4 steps with 9 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education

Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education

Control Systems Engineering
Mechanical Engineering
ISBN:
9781118170519
Author:
Norman S. Nise
Publisher:
WILEY

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning

Engineering Mechanics: Statics
Mechanical Engineering
ISBN:
9781118807330
Author:
James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:
WILEY