Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
Help me please 67,73,79,85

Transcribed Image Text:154 CHAPTER 3 Linear and Quadratic Functidl1s
63.
(c) At what horizontal distance from the face of the ali
(f) When the height of the projectile is 100 feet aboe
In Problems 65–72, determine, without graphing, whether the given quadratic function has a maximum value or a minimum value
(e) Use a graphing utility to verify the solutions foun
at an inclination of 45° to the horizontal, with a m
velocity of 100 feet per second. The height h of the pro
where x is the horizontal distance of the projectile fr
86. Analyzing the Motion of a Projectile A projectile is
74. The graph of the function f(x) = ax² + bx + chas w
64.
Vertex: (-2, 6)
8
(а)
62.
6
(3, 5).
41
Vertex: (2, 3)
(b)
(с)
2
5 X
2
3
-3
-1
(0, -1)
-4, -2)
(d)
(e)
(f)
-4- Vertex: (1, -3)
87. Ma
of
67. f(x) = 2x² + 12r – 3
71. f(x) = -5x² + 20x + 3
68. f(x) = 4x² - &x + 1
72. f(x) = 4x² – 4r
is
66. f(x) = -2r² + 12x
70. f(x) = -2r² + &r + 3
then find the value.
65. f(x) = 3x? + 24x
69. f(x) = -x²+ 6x – 1
W
re
Applications and Extensions
88. M
fo
73. The graph of the function f(x) = ax² + bx + c has vertex
at (0, 2) and passes through the point (1, 8). Find a, b,
and c.
at (1, 4) and passes through the point (-1, -8). F
m
and c.
ch
In Problems 75-80, for the given functions f and g:
A (a) Graph f and g on the same Cartesian plane.
(b) Solve f(x) = g(x).
(c) Use the result of part (b) to label the points of intersection of the graphs of f and g.
(d) Shade the region for which f(x) > g(x); that is, the region below f and above g.
75. f(x) = 2x – 1; g(x) = x² – 4
77. f(x) = -x² + 4; g(x) = -2x + 1
79. f(x) = -x² + 5x; g(x) = x? + 3x – 4
89. M
76. f(x) = -2x – 1; g(x) = x² - 9
78. f(x) = -x2 + 9; g(x) = 2x + 1
80. f(x) = -x² + 7x 6; g(x) = x² + x – 6
th
For Problems 81 and 82, use the fact that a quadratic function of the form f(x) = ax² + bx c with b? – 4ac > 0 may also be wi
in the form f(x) = a(x – r1) (x - r2), where r and r, are the x-intercepts of the graph of the quadratic function.
81. (a) Find quadratic functions whose x-intercepts are -3\ 85. Analyzing the trotion of a Projectile A projectile isfi
from a cliff 200 feet above the water at an inclination di
to the horizontal, with a muzzle velocity of 50 feet persam
The height h of the projectile above the water is modelei
and 1 with a = 1; a = 2; a = -2; a = 5.
(b) How does the value of a affect the intercepts?
(c) How does the value of a affect the axis of symmetry?
90,
(d) How does the value of a affect the vertex?
(e) Compare the x-coordinate of the vertex with the
midpoint of the x-intercepts. What might you conclude?
82. (a) Find quadratic functions whose x-intercepts are -5
and 3 with a = 1; a = 2; a = -2; a = 5.
(b) How does the value of a affect the intercepts?
(c) How does the value of a affect the axis of symmetry?
- 32.x?
+ x + 200
502
h(x) =
where x is the horizontal distance of the projectile ne
face of the cliff.
(a) At what horizontal distance from the face of the
the height of the projectile a maximum?
(b) Find the maximum height of the projectile.
(d) How does the value of a affect the vertex?
91.
(e) Compare the x-coordinate of the vertex with the
midpoint of the x-intercepts. What might you conclude?
83. Suppose that f(x) = x² + 4x – 21.
(a) What is the vertex of f?
(b) What are the x-intercepts of the graph of f?
(c) Solve f(x) = -21 for x. What points are on the graph
of f?
(d) Use the information obtained in parts (a)-(c) to
graph f(x) = x² + 4x – 21.
84. Suppose that f(x) = x² + 2x – 8.
(a) What is the vertex of f?
(b) What are the x-intercepts of the graph of f?
(c) Solve f(x) = -8 for x. What points are on the graph
the projectile strike the water?
(d) Graph the function h,0 < x< 200.
parts (b) and (c).
water, how far is it from the cliff?
is modeled by
of f?
(d) Use the information obtained in parts (a)-(c) to
graph f(x) = x² + 2x – 8.
92
h(x)
- 32x?
+ x
1002
firing point
Expert Solution
Step 1
Since you have asked multiple questions in a single request so we will be answering only first question.
..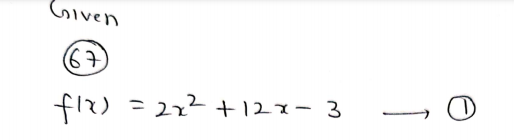
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning