6. Sketch the graph of y= Cos (0.5x + 20m) from x = -2π to x = 2π
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Problem 6: Sketch the Graph of y = Cos(0.5x + 20π)**
**Instructions:**
- Sketch the graph of the function \( y = \cos(0.5x + 20\pi) \).
- Consider the interval from \( x = -2\pi \) to \( x = 2\pi \).
**Graph Explanation:**
The image contains a Cartesian plane featuring an x-axis labeled with increments of \( \pi \), ranging from \( -2\pi \) to \( 2\pi \). The y-axis is oriented upright, intersecting the x-axis at the origin (0,0). Both axes are marked, but the sketch of the cosine function is not displayed.
**Key Considerations:**
- **Amplitude:** The amplitude of the cosine function is 1.
- **Period:** The coefficient of x is 0.5, affecting the period of the function. The period \( T \) is calculated as \( T = \frac{2\pi}{0.5} = 4\pi \).
- **Phase Shift:** The phase shift is determined by the constant term inside the cosine function, \( 20\pi \), which results in no visible shift as it is a multiple of \( 2\pi \).
- **Sketching Steps:**
1. Identify critical points where \( y = 1, 0, -1 \).
2. Recognize that due to the period adjustment, one full cycle of the cosine curve spans from 0 to \( 4\pi \).
3. Plot the corresponding y-values at significant x-values within the specified range.
By sketching this function, students can visualize how changes in coefficients and constants inside trigonometric functions modify their graphs.
Expert Solution
Introduction
Cosine graph:
The cosine graph is up and down graph i.e.
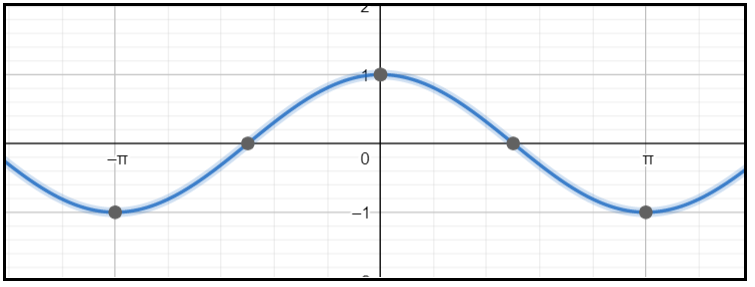
The cosine graph is always between -1 and 1.
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

