6. For A, B C R, define A + B = {a+b: a € A, b € B} A B = {a -b: a € A, b E B} %3D (i) Determine {3, 1,0} + {2,0, 2, 1} and {3, 1,0} {2,0, 2, 1}
6. For A, B C R, define A + B = {a+b: a € A, b € B} A B = {a -b: a € A, b E B} %3D (i) Determine {3, 1,0} + {2,0, 2, 1} and {3, 1,0} {2,0, 2, 1}
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%
Problem 6. (i) please!

Transcribed Image Text:inf(A) = -sup(-A)
4. Let A = {, ne N}. Prove that sup(A) = 1, inf(A) = .
5. (i) Let A, BCR be sets which are bounded above, such that A C B. Show that sup(A) < sup
(ii) Let A, BCR such that sup(A) < sup(B). Show that there exists b E B that is an upper b0
Show that this result does not hold if we instead assume that sup(A) < sup(B).
6. For A, B CR, define
A + B = {a+b:a E A, b E B}
A·B = {a -b: a E A, b E B}
(i) Determine {3, 1,0} + {2,0, 2, 1} and {3, 1,0} {2,0, 2, 1}
(ii) Assume that sup(A) and sup(B) exist. Prove that sup(A+ B) = sup(A) + sup(B).
(iii) Give an example of sets A, B where sup(A B) + sup(A) - sup(B)
!!
Warm-up Problems, Not for credit:
1. Let F be any field. Prove that both the additive and multiplicative identities in F are unique.
2. Given an ordered field F, we saw that it has a set of positive elements P satisfying certain two
입력하십시오.
LG
Expert Solution
Step 1
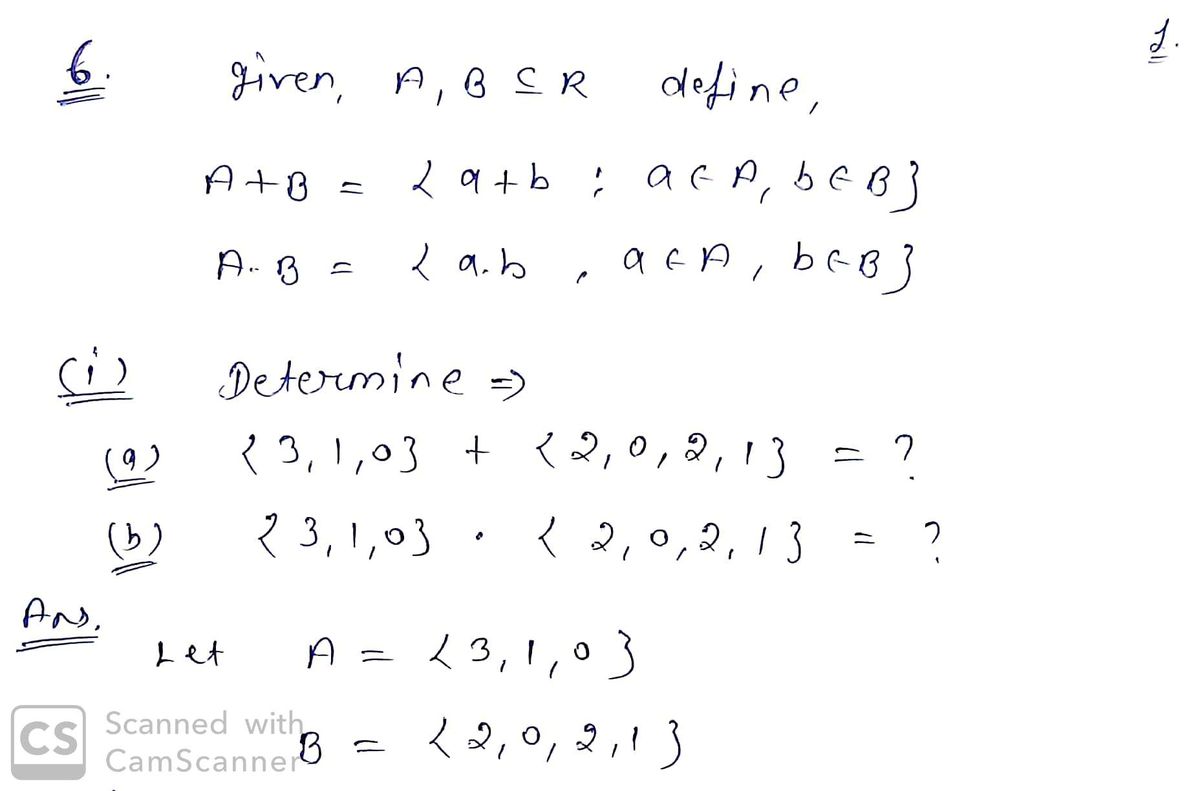
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

