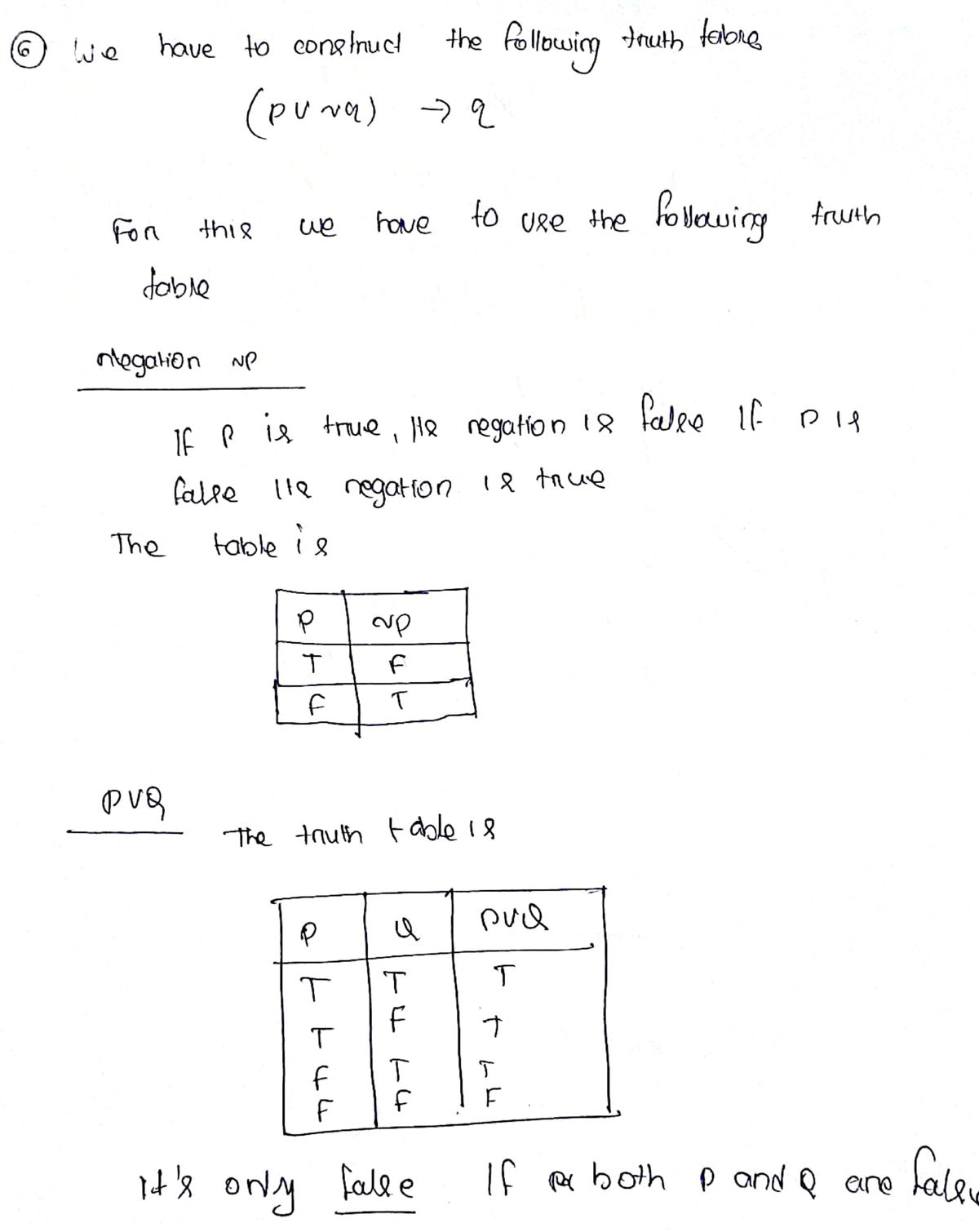
6. Construct a truth table for the following statement. (p V ~q) → 9
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Certainly! Below is a transcription suitable for an educational website:
---
**Exercise 6.**
Construct a truth table for the following statement:
\((p \lor \sim q) \rightarrow q\)
---
To solve this, start by considering the logical operators involved:
1. **Disjunction (\(\lor\))**: This operator is true if at least one of the operands is true.
2. **Negation (\(\sim\))**: This operator inverts the truth value of its operand.
3. **Implication (\(\rightarrow\))**: This operator is false only when the first operand is true and the second operand is false.
The truth table will examine all possible truth values of \(p\) and \(q\):
| \(p\) | \(q\) | \(\sim q\) | \(p \lor \sim q\) | \((p \lor \sim q) \rightarrow q\) |
|-------|-----|------|-----------------|-------------------------|
| T | T | F | T | T |
| T | F | T | T | F |
| F | T | F | F | T |
| F | F | T | T | F |
Explanation of each column:
- **\(p\) and \(q\)**: Initial truth values we are considering.
- **\(\sim q\)**: The negation of \(q\).
- **\(p \lor \sim q\)**: The result of the disjunction between \(p\) and \(\sim q\).
- **\((p \lor \sim q) \rightarrow q\)**: The final implication we want to evaluate.
This table effectively illustrates both the intermediate logical outcomes and the final conclusion of the statement for all possible logical inputs.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

