Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![**Problem 6: Prove the Trigonometric Identity**
Prove that:
\[ \cos^4 x - \sin^4 x = \cos 2x \]
This is a trigonometric identity that demonstrates the relationship between the fourth powers of sine and cosine functions and the double angle cosine. To prove this identity, utilize trigonometric identities and algebraic manipulation.
**Solution Outline:**
1. Start with the left side of the equation, \( \cos^4 x - \sin^4 x \).
2. Use the difference of squares identity:
\[ a^2 - b^2 = (a - b)(a + b) \]
Thus, express \( \cos^4 x - \sin^4 x \) as:
\[ (\cos^2 x - \sin^2 x)(\cos^2 x + \sin^2 x) \]
3. Recall the Pythagorean identity:
\[ \cos^2 x + \sin^2 x = 1 \]
Substitute this into the expression:
\[ (\cos^2 x - \sin^2 x)(1) = \cos^2 x - \sin^2 x \]
4. Use the double angle identity for cosine:
\[ \cos 2x = \cos^2 x - \sin^2 x \]
Conclude that:
\[ \cos^4 x - \sin^4 x = \cos 2x \]
This demonstrates the correctness of the identity through algebraic manipulation and application of known trigonometric identities.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fe708b20e-246d-43f9-aec0-b076b54d250e%2F93f55d8c-62ee-48df-8ea2-9c94d40447b8%2Fxiscdc_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem 6: Prove the Trigonometric Identity**
Prove that:
\[ \cos^4 x - \sin^4 x = \cos 2x \]
This is a trigonometric identity that demonstrates the relationship between the fourth powers of sine and cosine functions and the double angle cosine. To prove this identity, utilize trigonometric identities and algebraic manipulation.
**Solution Outline:**
1. Start with the left side of the equation, \( \cos^4 x - \sin^4 x \).
2. Use the difference of squares identity:
\[ a^2 - b^2 = (a - b)(a + b) \]
Thus, express \( \cos^4 x - \sin^4 x \) as:
\[ (\cos^2 x - \sin^2 x)(\cos^2 x + \sin^2 x) \]
3. Recall the Pythagorean identity:
\[ \cos^2 x + \sin^2 x = 1 \]
Substitute this into the expression:
\[ (\cos^2 x - \sin^2 x)(1) = \cos^2 x - \sin^2 x \]
4. Use the double angle identity for cosine:
\[ \cos 2x = \cos^2 x - \sin^2 x \]
Conclude that:
\[ \cos^4 x - \sin^4 x = \cos 2x \]
This demonstrates the correctness of the identity through algebraic manipulation and application of known trigonometric identities.
Expert Solution
Step 1
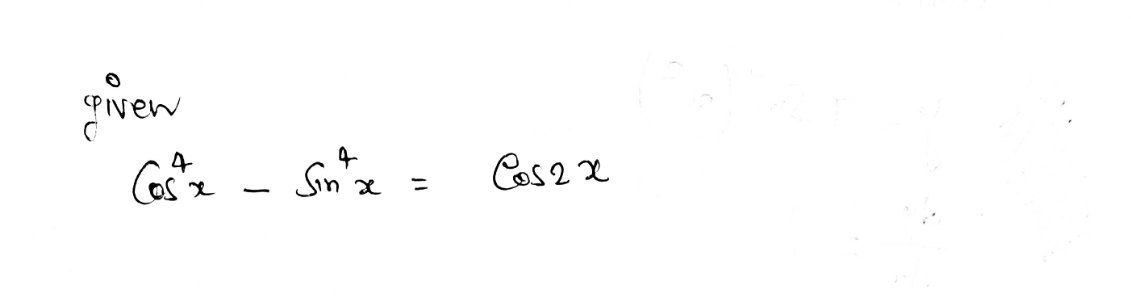
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning