Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
(6) Define the center of a group G as the subset Z = {z EG: zg = gz for all g € G}. Prove that Z is a normal subgroup of G.

(6) Define the center of a group G as the subset Z = {z EG: zg = gz for all g € G}. Prove that Z is a normal subgroup of G.

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question

Abstract Algebra I 

1. Show that \( S_4 \) does not contain a normal subgroup of order 2. 2. Define the *center* of a group \( G \) as the subset \[ Z = \{ z \in G : zg = gz \text{ for all } g \in G \}. \] Prove that \( Z \) is a normal subgroup of \( G \).
Transcribed Image Text:1. Show that \( S_4 \) does not contain a normal subgroup of order 2. 2. Define the *center* of a group \( G \) as the subset \[ Z = \{ z \in G : zg = gz \text{ for all } g \in G \}. \] Prove that \( Z \) is a normal subgroup of \( G \).
Expert Solution
Step 1

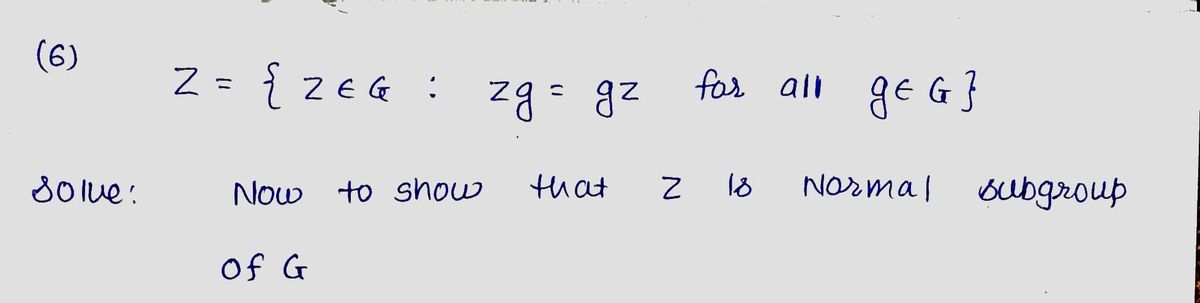
Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS