-5/4 -TT -3/4 -TT/2 -TT/4 -7- -6 TT/4 TT/2 c. Give the midline (vertical shift) of the function. 3TT/4 a. On the graph shown, highlight one period of the function. b. Give the period of this function. TT 57/4
-5/4 -TT -3/4 -TT/2 -TT/4 -7- -6 TT/4 TT/2 c. Give the midline (vertical shift) of the function. 3TT/4 a. On the graph shown, highlight one period of the function. b. Give the period of this function. TT 57/4
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:The provided image contains a mathematical task related to trigonometric functions, specifically a sine or cosine graph. Below is a detailed transcription of the content along with explanations of the graph:
### Task:
1. **Graph Description:**
- The graph shows a periodic sine wave with intervals marked along the x-axis from \(-5\pi/4\) to \(5\pi/4\).
- The y-axis is marked from -1 to 8, and the wave oscillates between these points.
- One full period of the sine wave starts at \(-\pi\), crosses the x-axis at the origin (0), and ends at \(\pi\).
2. **Questions and Answers:**
a. **On the graph shown, highlight one period of the function.**
- **Explanation:** A period of the function is the length along the x-axis where the wave completes one full cycle. This is from \(-\pi\) to \(\pi\).
b. **Give the period of this function.**
- **Answer:** \(\pi\)
- **Explanation:** The period is the distance the wave takes to repeat its pattern, which is \(\pi\) in this graph.
c. **Give the midline (vertical shift) of the function.**
- **Explanation:** The midline is the horizontal line that runs through the middle of the wave. It is not explicitly given in the image but can be deduced from the amplitude spanning from -1 to 7.
d. **Give the amplitude of the function.**
- **Answer:** Amplitude = 3
- **Explanation:** The amplitude is the distance from the midline to the peak, which is 3 units.
e. **Find an equation for this graph of the form \( f(x) = a \sin(b(x-c)) + d \) (Bonus points if you can give more than one answer!)**
- **Answer:** \(3\sin(\pi x)\)
- **Explanation:** The equation represents a sine function with an amplitude of 3.
f. **Find an equation for this graph of the form \( f(x) = a \cos(b(x-c)) + d \)**
- **Explanation:** This requires transforming the given sine equation into a cosine form, considering any phase shift, but a specific answer is not provided.
### Graph
Expert Solution
Step 1
As per the policy of bartleby the provisions is to solve only three sub parts of questions now I am solving a, b and c 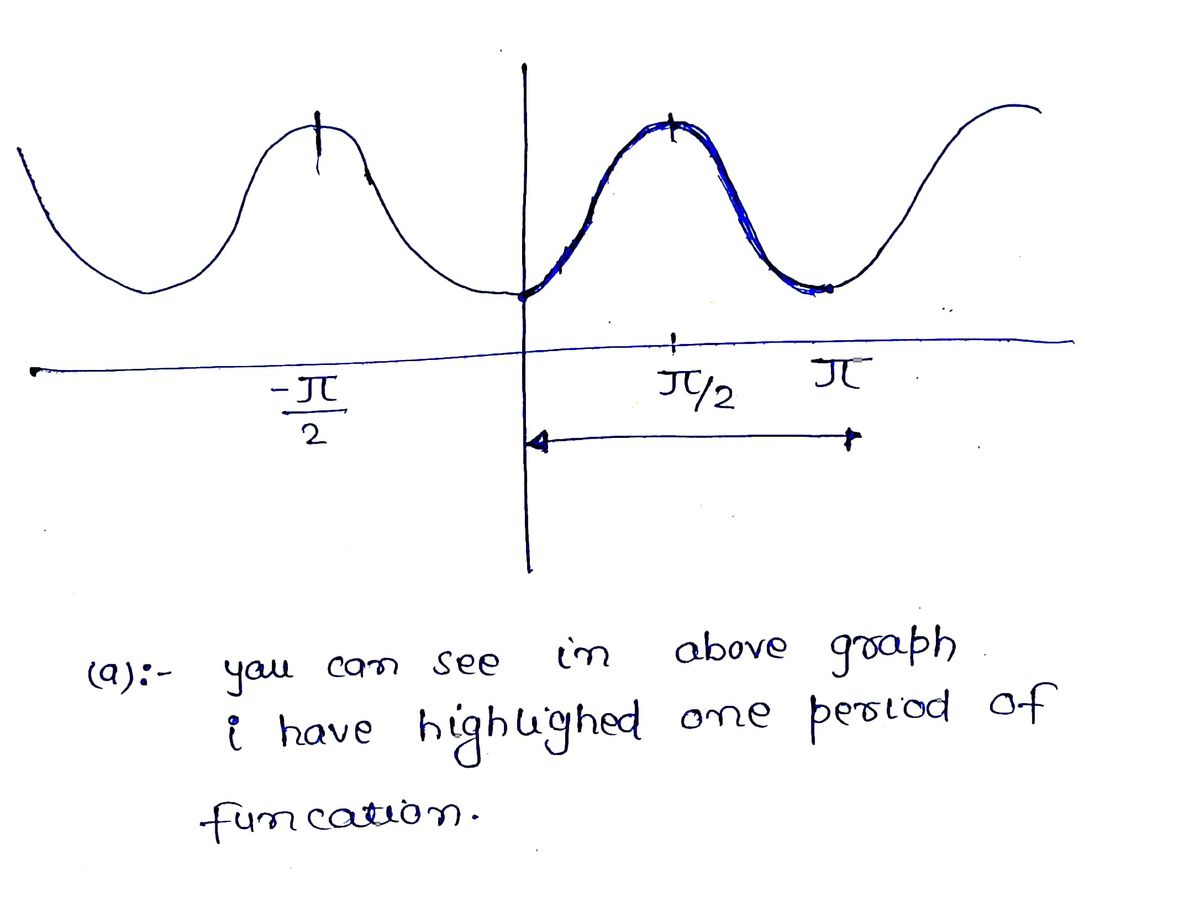
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

