Can you help with 16 please? 5.3 Path Integrals of Vector Fields32515. Suppose that a continuous function f is integrated along two different paths joining the points(1, 2) and (3, -5), and two different answers are obtained. Is that possible, or has an error been madein the evaluation of integrals?16. Compute the integral of f(x, y) = xy – x - y +1 along the following curves connecting thepoints (1, 0) and (0, 1):(a) C1: circular arc c1(t) = (cos t, sin t), 0 < t

Name: Can you help with 16 please? 5.3 Path Integrals of Vector Fields32515.
Uploaded: 2024-03-20T07:07:37.000Z
Channel: Bartleby
Description: Can you help with 16 please? 5.3 Path Integrals of Vector Fields32515. Suppose that a continuous function f is integrated along two different paths joining the points(1, 2) and (3, -5), and two different answers are obtained. Is that possible, or has

Answered: 5.3 Path Integrals of Vector Fields 325…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Topic Video

Question

Can you help with 16 please?

5.3 Path Integrals of Vector Fields
325
15. Suppose that a continuous function f is integrated along two different paths joining the points
(1, 2) and (3, -5), and two different answers are obtained. Is that possible, or has an error been made
in the evaluation of integrals?
16. Compute the integral of f(x, y) = xy – x - y +1 along the following curves connecting the
points (1, 0) and (0, 1):
(a) C1: circular arc c1(t) = (cos t, sin t), 0 < t <T/2
(b) c2: straight-line segment c2(t) = (1 – t, t), 0 <t < 1
(c) C3: from (1, 0) horizontally to the origin, then vertically to (0, 1)
(d) C4: from (1, 0) vertically to (1, 1), then horizontally to (0, 1)
(e) c5: circular arc c5(t) = (cos t, - sin t), 0 <t < 3n/2.
%3D
17. Compute the area of the part of the cylinder x? + y² = 4 between the xy-plane and the plane
Z = y +2.
%3D
18. Compute the area of the part of the surface y =x defined by 0 <x < 2,0 <:s2.
%3D
19. Compute the area of the part of the surface y = sin x, 0 <x </2, above the xy-plane and
below the surface z = sin x cos x.
%3D
20. Let e be the straight-line segment joining (1, 0, 0) and (0, 2, 0), Use a geometric argument (i.e.,
do not evaluate the integral) to find (x+3y) ds.
21. Use a geometric argument to find ety ds, where e is the circle centered at the origin of
radius 4.
22. Argue geometrically that , sin (x') ds 2 0, wherec is the graph of y= tan.x,-7/4 sx S/4.
23. Is it possible that the average value of f(x, y) = sinx cos y along some curve e is equal to 5?
24, Write down the version of the statement of Theorem 5.2 in the case where e is a piecewise C!

Expert Solution

Step 1

Hey, since there are multiple sub-parts posted, we will answer first three sub-parts . If you want any specific question to be answered then please submit that question only or specify the question number in your message.

Step 2

Step 3

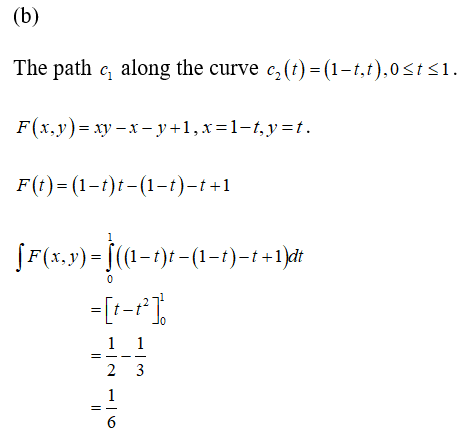
Step by step

Solved in 5 steps with 4 images

Knowledge Booster

$Research Design Formulation$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions