Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
5. In future courses, you'll meet sequences of functions. For instance, consider we could define a sequence (fn) of functions fn: R→ R inductively via fo(x) = 1, fn+1(x) :=1+ for fn (1) dt Compute the functions f₁, f2 and f3. The sequence (fn) should seem familiar if you think back to elementary calculus; why?

5. In future courses, you'll meet sequences of functions. For instance, consider we could define a sequence (fn) of functions fn: R→ R inductively via fo(x) = 1, fn+1(x) :=1+ for fn (1) dt Compute the functions f₁, f2 and f3. The sequence (fn) should seem familiar if you think back to elementary calculus; why?

Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter3: Functions And Graphs
Section3.2: Graphs Of Equations
Problem 78E
See similar textbooks
icon
Related questions
Question
5. In future courses, you’ll meet sequences of *functions*. For instance, consider we could define a sequence \((f_n)\) of functions \(f_n : \mathbb{R} \to \mathbb{R}\) inductively via \[ f_0(x) \equiv 1, \quad f_{n+1}(x) := 1 + \int_0^x f_n(t) \, dt \] Compute the functions \(f_1, f_2\) and \(f_3\). The sequence \((f_n)\) should seem familiar if you think back to elementary calculus; why?
Transcribed Image Text:5. In future courses, you’ll meet sequences of *functions*. For instance, consider we could define a sequence \((f_n)\) of functions \(f_n : \mathbb{R} \to \mathbb{R}\) inductively via \[ f_0(x) \equiv 1, \quad f_{n+1}(x) := 1 + \int_0^x f_n(t) \, dt \] Compute the functions \(f_1, f_2\) and \(f_3\). The sequence \((f_n)\) should seem familiar if you think back to elementary calculus; why?
Expert Solution
Step 1: f1 and f2

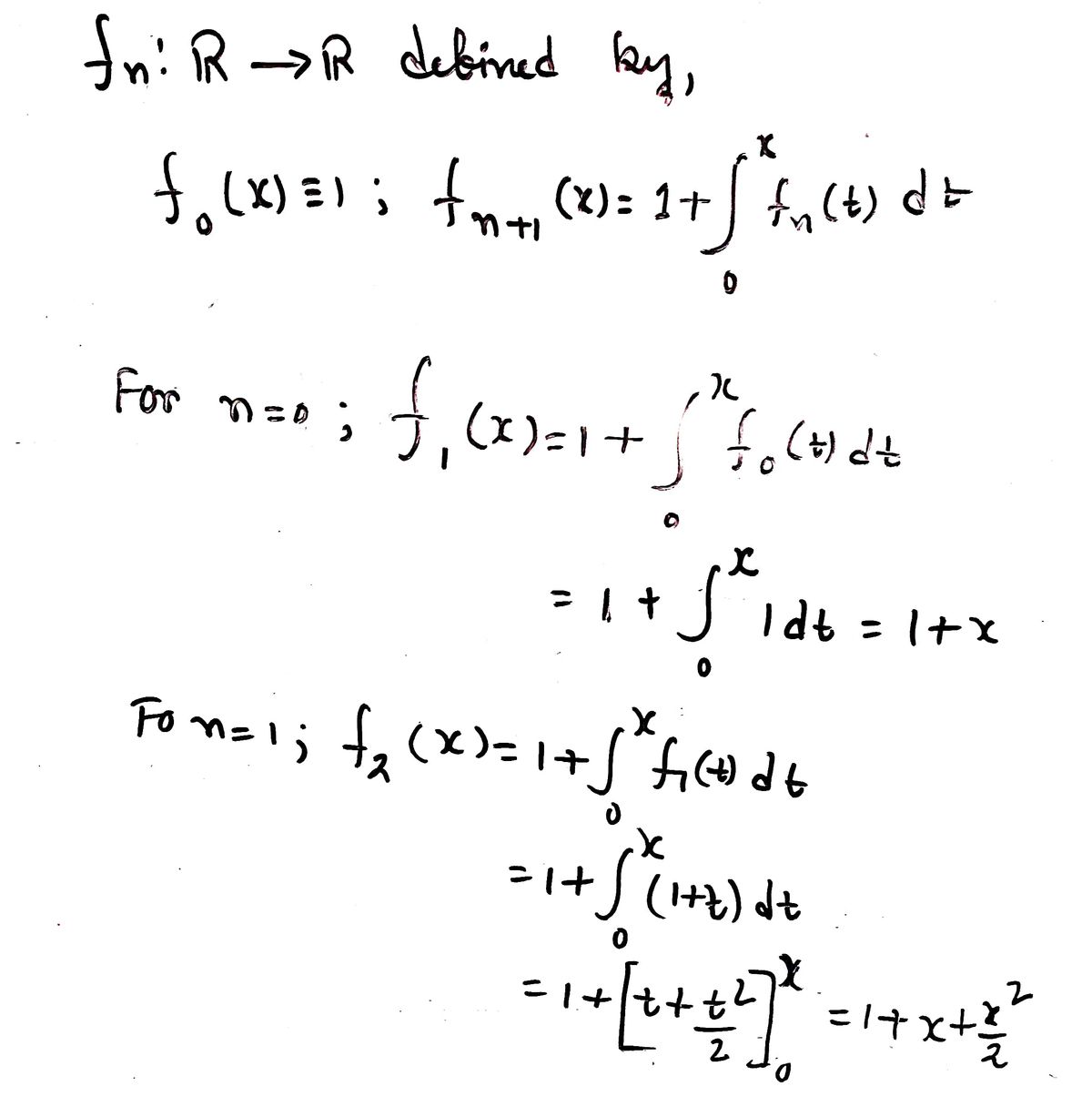
Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 3 steps with 3 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer