5. Assume that an ant moves on a plane continuously; that is, its coordinates x(t) and y(t) are continuous functions of time t. The ant starts moving from the point (0.7, 0.1) and arrives at (-2,3) five minutes later. Prove that the ant has at least once crossed (a) the unit circle, (b) the perimeter of the square [-1, 1] × [–1, 1], (c) the perimeter of the diamond shape {(x, y) : |æ| + \y] < 1}.
5. Assume that an ant moves on a plane continuously; that is, its coordinates x(t) and y(t) are continuous functions of time t. The ant starts moving from the point (0.7, 0.1) and arrives at (-2,3) five minutes later. Prove that the ant has at least once crossed (a) the unit circle, (b) the perimeter of the square [-1, 1] × [–1, 1], (c) the perimeter of the diamond shape {(x, y) : |æ| + \y] < 1}.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Real An
![5. Assume that an ant moves on a plane continuously; that is, its coordinates
x(t) and y(t) are continuous functions of time t. The ant starts moving from
the point (0.7, 0.1) and arrives at (-2,3) five minutes later. Prove that the
ant has at least once crossed
(a) the unit circle,
(b) the perimeter of the square [–1, 1] × [–1, 1],
(c) the perimeter of the diamond shape {(x, y) : |x| + \y] < 1}.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F7fd47556-f3ce-4f39-818d-be563d9523c8%2Fbd0ace01-093b-4355-8d9e-c369e846c904%2F9515yue_processed.png&w=3840&q=75)
Transcribed Image Text:5. Assume that an ant moves on a plane continuously; that is, its coordinates
x(t) and y(t) are continuous functions of time t. The ant starts moving from
the point (0.7, 0.1) and arrives at (-2,3) five minutes later. Prove that the
ant has at least once crossed
(a) the unit circle,
(b) the perimeter of the square [–1, 1] × [–1, 1],
(c) the perimeter of the diamond shape {(x, y) : |x| + \y] < 1}.
Expert Solution
Step 1
(a)
equation of unit circle can be written as -
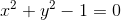
at (0.7,0.1)
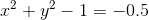
at (-2,3)
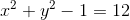
we see the change in sign from [0.7,0.1] to [-2,3]. It means both points are located on opposite side of curve.
(b)
perimeter of [-1,1]*[-1,1]
we can see that (0.7,0.1) is inside above curve and (-2,3) is outside the curve. So ant will definately cross the perimeter.
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

