49. If two objects travel through space along two different curves, it's often important to know whether they will col- lide. (Will a missile hit its moving target? Will two aircraft collide?) The curves might intersect, but we need to know whether the objects are in the same position at the same time. Suppose the trajectories of two particles are given by the vector functions 150 r₁(t) = (t², 7t for t≥ 0. Do the particles - 12, t²) r₂(t) = (4t-3, t², 5t - 6) collide?
49. If two objects travel through space along two different curves, it's often important to know whether they will col- lide. (Will a missile hit its moving target? Will two aircraft collide?) The curves might intersect, but we need to know whether the objects are in the same position at the same time. Suppose the trajectories of two particles are given by the vector functions 150 r₁(t) = (t², 7t for t≥ 0. Do the particles - 12, t²) r₂(t) = (4t-3, t², 5t - 6) collide?
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
49

Transcribed Image Text:Then find para
equations and a computer to graph the curve.
48. Try to sketch by hand the curve of intersection of the
parabolic cylinder y = x² and the top half of the ellipsoid
x² + 4y² + 4z² = 16. Then find parametric equations for
this curve and use these equations and a computer to graph
the curve.
49. If two objects travel through space along two different
curves, it's often important to know whether they will col-
lide. (Will a missile hit its moving target? Will two aircraft
collide?) The curves might intersect, but we need to know
whether the objects are in the same position at the same
time. Suppose the trajectories of two particles are given by
the vector functions
r₁(t) = (t², 7t - 12, t²)
for t≥ 0. Do the particles collide?
50. Two particles travel along the space curves
r₂(t) = (4t-3, t², 5t - 6)
10
r₂(t) = (1 + 2t, 1 + 6t, 1 + 14t)
r₁(t) = (t, t², t³)
Do the particles collide? Do their paths intersect?
13.2 Derivatives and Integrals of Vector Fun-
Later in this chapter we are
Expert Solution
Step 1
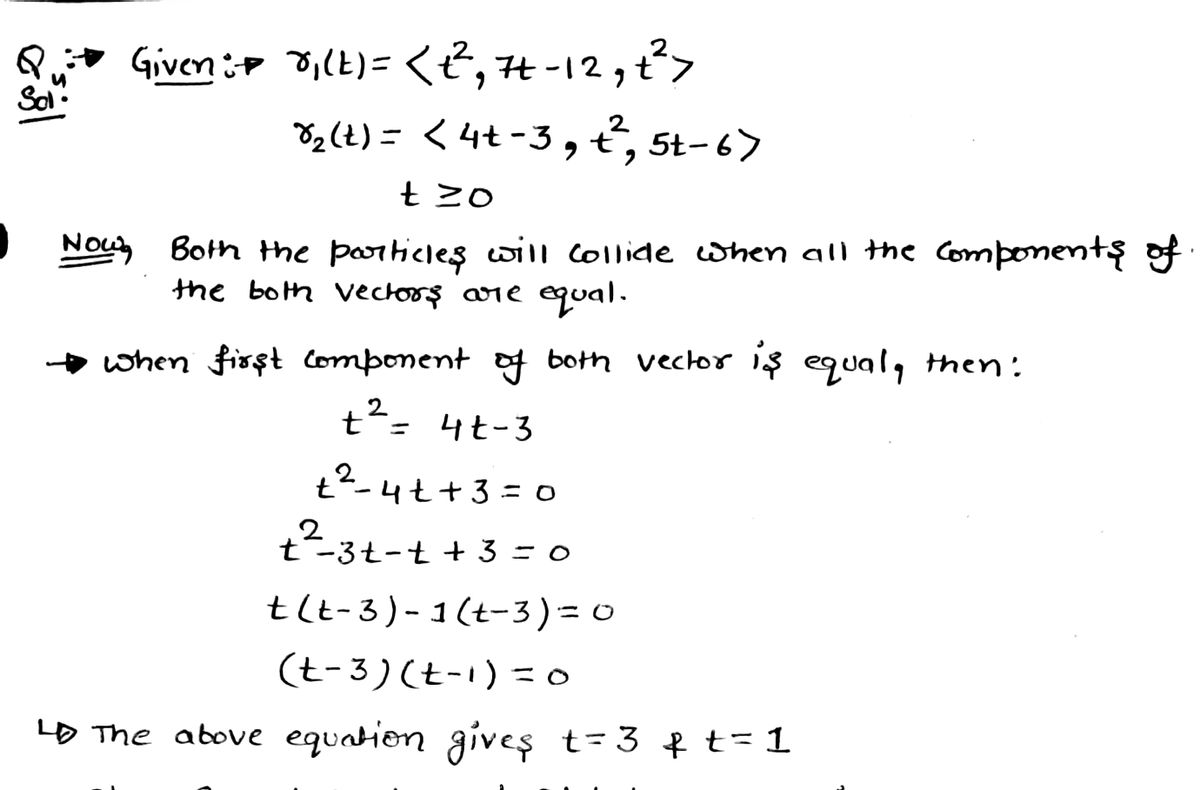
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning