40.10894 C5 40.11267 40.02465 Mean 40.02725817 39.90825 Standard Error 0.025458932 40.09327 Median 40.03340699 40.01079 Mode #N/A 40.17161 Standard Deviation 0.098602021 40.15561 Sample Variance 0.009722359 40.05552 Kurtosis -0.553062099 39.976 Skewness -0.421387838 39.92105 Range 0.341306053 40.07877 Minimum 39.83030789 39.92803 Maximum 40.17161394 40.03341 Sum 600.4088725 39.83031 Count 15 40.02726 Confidence Level(95.0%) 0.054603979
C5 - These are the machined inner diameters in mm for gear samples provided by a new supplier that we are considering. The target diameter is 40.05 mm. Does the new supplier meet the target inner diameter (is it safe to say that the population
Interpret the following set of data using one sample
Data sets:
| C5 | |||
| 40.10894 | C5 | ||
| 40.11267 | |||
| 40.02465 | Mean | 40.02725817 | |
| 39.90825 | Standard Error | 0.025458932 | |
| 40.09327 | 40.03340699 | ||
| 40.01079 | #N/A | ||
| 40.17161 | Standard Deviation | 0.098602021 | |
| 40.15561 | Sample Variance | 0.009722359 | |
| 40.05552 | Kurtosis | -0.553062099 | |
| 39.976 | Skewness | -0.421387838 | |
| 39.92105 | 0.341306053 | ||
| 40.07877 | Minimum | 39.83030789 | |
| 39.92803 | Maximum | 40.17161394 | |
| 40.03341 | Sum | 600.4088725 | |
| 39.83031 | Count | 15 | |
| 40.02726 | Confidence Level(95.0%) | 0.054603979 |
The following hypothesis can be constructed to test whether the supplier meet the target. The supplier will meet the target when mean inner diameter is at least 40.05mm.
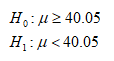
The level of significance is given as 5%. So, the critical value from t-table at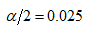 
level with n-1 =14 degree of freedom is 2.1447.
Step by step
Solved in 2 steps with 3 images
