Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
How do I solve this derivative equation when it is equal to 0
![(a) **What is the derivative of \( y(t) \)?**
\[ y'(t) = \frac{1}{2} \cos(t) - \frac{t}{2} \sin(t) \]
(b) **Places where a derivative is 0 are places where the function has a horizontal tangent line. Set the derivative equal to 0 and solve for \( t \). There are infinitely many solutions. Ask WolframAlpha to solve the equation that you have. What are the solutions with \( t < 10 \) (round to the nearest tenth)?**
\[ 0 = -\frac{1}{2} \cos(t) - \frac{t}{2} \sin(t) \]
\[ 0 = \cos(t) - t \sin(t) \]
(c) **Suppose this is a model of a building experiencing resonance as it sways back and forth in an earthquake. What is the building doing at the times you found in part (b)?**
---
**Graph Explanation:**
There is a small graph visible at the top left corner of the image. It appears to be a plot of a function over a certain domain, likely representing the solution or behavior described in the problem. The x-axis likely represents time \( t \) while the y-axis represents the value of \( y(t) \) or its derivative. However, without more detail, we cannot specify the exact function plotted.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F051d9a8d-fe28-4947-87a7-657149e37dc8%2F5842bda4-be35-4209-a461-914ff392e967%2F43mxwpc_processed.jpeg&w=3840&q=75)
Transcribed Image Text:(a) **What is the derivative of \( y(t) \)?**
\[ y'(t) = \frac{1}{2} \cos(t) - \frac{t}{2} \sin(t) \]
(b) **Places where a derivative is 0 are places where the function has a horizontal tangent line. Set the derivative equal to 0 and solve for \( t \). There are infinitely many solutions. Ask WolframAlpha to solve the equation that you have. What are the solutions with \( t < 10 \) (round to the nearest tenth)?**
\[ 0 = -\frac{1}{2} \cos(t) - \frac{t}{2} \sin(t) \]
\[ 0 = \cos(t) - t \sin(t) \]
(c) **Suppose this is a model of a building experiencing resonance as it sways back and forth in an earthquake. What is the building doing at the times you found in part (b)?**
---
**Graph Explanation:**
There is a small graph visible at the top left corner of the image. It appears to be a plot of a function over a certain domain, likely representing the solution or behavior described in the problem. The x-axis likely represents time \( t \) while the y-axis represents the value of \( y(t) \) or its derivative. However, without more detail, we cannot specify the exact function plotted.
Expert Solution
Step 1
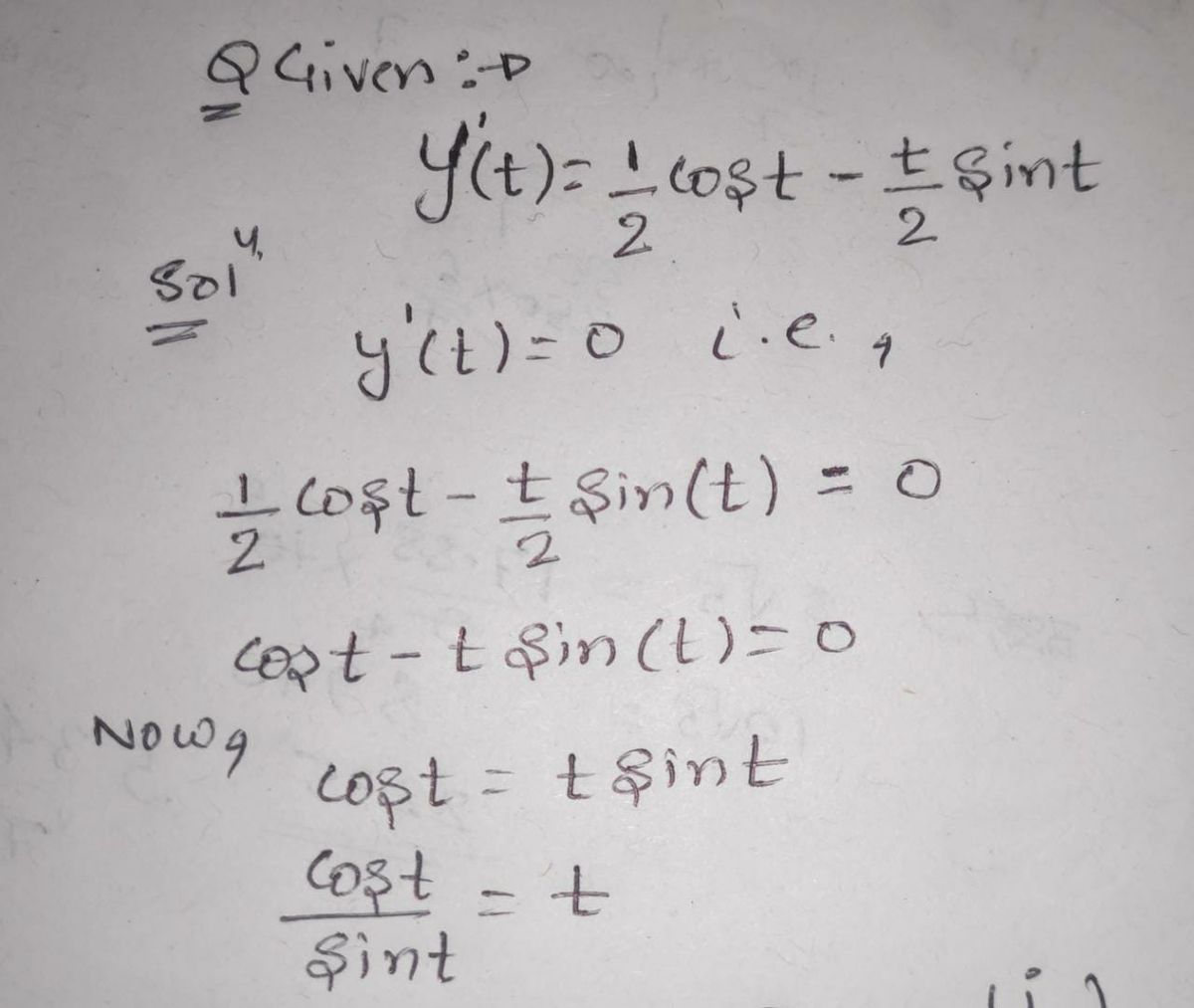
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning