1. 4.3/4.7: A rectangle is inscribed in the ellipse+y² a) Find the minimum possible area of the rectangle. (b) Find the maximum possible area of the rectangle. (c) Find the maximum possible perimeter of the rectangle.
1. 4.3/4.7: A rectangle is inscribed in the ellipse+y² a) Find the minimum possible area of the rectangle. (b) Find the maximum possible area of the rectangle. (c) Find the maximum possible perimeter of the rectangle.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Title: Problem 4.3/4.7 - Rectangle Inscribed in an Ellipse**
A rectangle is inscribed in the ellipse characterized by the equation \(\frac{x^2}{4} + \frac{y^2}{1} = 1\).
**Tasks:**
1. **Find the minimum possible area of the rectangle.**
2. **Find the maximum possible area of the rectangle.**
3. **Find the maximum possible perimeter of the rectangle.**
**Solution Steps:**
The problem involves finding specific attributes of a rectangle inscribed in an ellipse with a given equation. The goal is to determine extreme values related to area and perimeter.
**Solution Diagram and Annotations:**
- On the right, there is a sketch of the ellipse and the rectangle inscribed within it. The ellipse is centered at the origin, extending horizontally to 2 units and vertically to 1 unit. The rectangle is shaded inside and aligned symmetrically with respect to both axes.
**Mathematical Analysis:**
- **Area Calculation:**
- The area of the rectangle \(A\) can be expressed as a function of \(x\):
\(A = 2x \cdot 2y\), where \(y = \sqrt{1 - \frac{x^2}{4}}\).
- Substituting \(y\), the area \(A = 2x \times 2\sqrt{1 - \frac{x^2}{4}}\).
- **Perimeter Calculation:**
- Not directly solved here, but involves using the expression for the perimeter \(P = 2(l + w)\), where \(l\) and \(w\) are the side lengths related to \(x\) and \(y\).
- **Further Annotations:**
- There are additional handwritten notes involving equations and calculations attempting to find extreme values using derivatives or completing the square.
- Computational steps involve manipulating the equation \(D^2 = (1 - \frac{x^2}{4})\).
This analysis allows a deeper understanding of the geometric properties of shapes inscribed within conic sections, specifically focusing on the ellipse and optimization problems related to area and perimeter.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
i didn't understand what he wrote for the answers
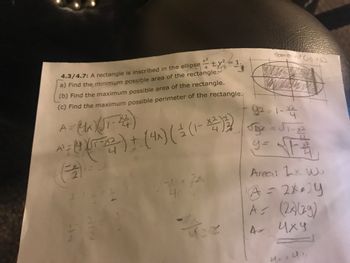
Transcribed Image Text:4
4.3/4.7: A rectangle is inscribed in the ellipse ±y ²
a) Find the minimum possible area of the rectangle:
(b) Find the maximum possible area of the rectangle.
(c) Find the maximum possible perimeter of the rectangle.
92
A=(1K) (UT-14)
(4 X
X2
^² = 0 (07-2² ) + ( 4^) ( ² (1-4)32)
2
니
4
2
2
NIN
NIN
D
4/
• ZA
1.
422
domain (< x≤2
Xn
92-1-23
Jy₂ = √₁-1²
y=√1₁₁
4
Area: Lx w
A = 2x014
A = (2x)(29)
иху
4. Ur.
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

