Homework Help is Here – Start Your Trial Now!
Math
Probability
4.20. Show that X is a Poisson random variable with parameter 1, then E[X¹] = λE[(X + 1)"−¹] Now use this result to compute E[X³].

4.20. Show that X is a Poisson random variable with parameter 1, then E[X¹] = λE[(X + 1)"−¹] Now use this result to compute E[X³].

A First Course in Probability (10th Edition)
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
See similar textbooks
icon
Related questions
Question

How to solve question 4.20?

**Transcription for Educational Purposes:** ### Section 4.20 **Problem Statement**: Show that if \( X \) is a Poisson random variable with parameter \( \lambda \), then: \[ E[X^n] = \lambda E[(X + 1)^{n-1}] \] **Instruction**: Now use this result to compute \( E[X^3] \). ### Section 4.21 **Problem Context**: Consider \( n \) coins, each of which independently comes up heads with probability \( p \). Suppose that \( n \) is large and \( p \) is small, and let \( \lambda = np \).
Transcribed Image Text:**Transcription for Educational Purposes:** ### Section 4.20 **Problem Statement**: Show that if \( X \) is a Poisson random variable with parameter \( \lambda \), then: \[ E[X^n] = \lambda E[(X + 1)^{n-1}] \] **Instruction**: Now use this result to compute \( E[X^3] \). ### Section 4.21 **Problem Context**: Consider \( n \) coins, each of which independently comes up heads with probability \( p \). Suppose that \( n \) is large and \( p \) is small, and let \( \lambda = np \).
Expert Solution
Step 1

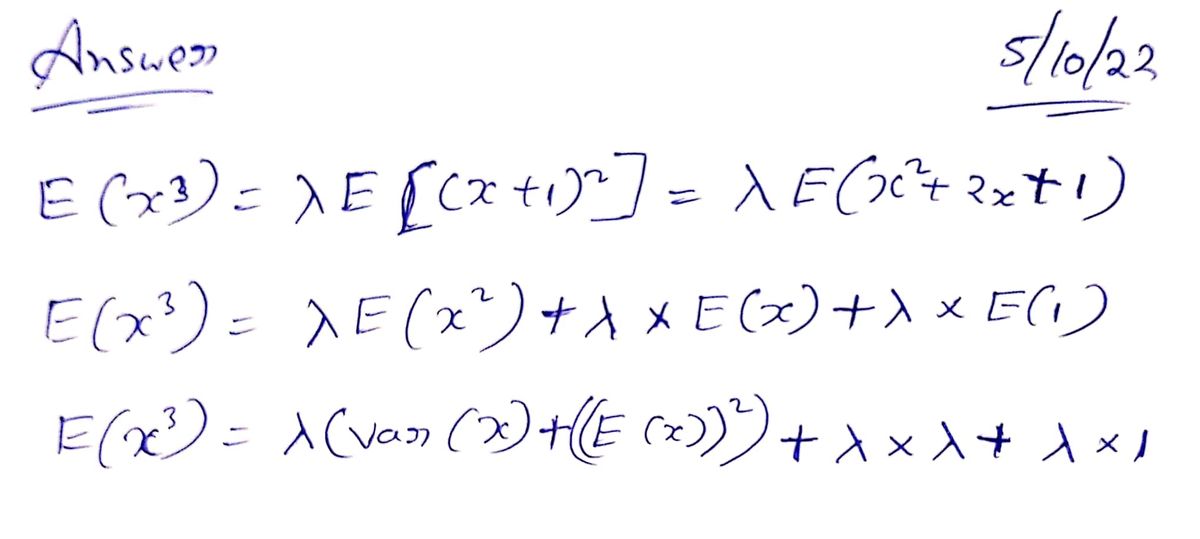
Probability homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer