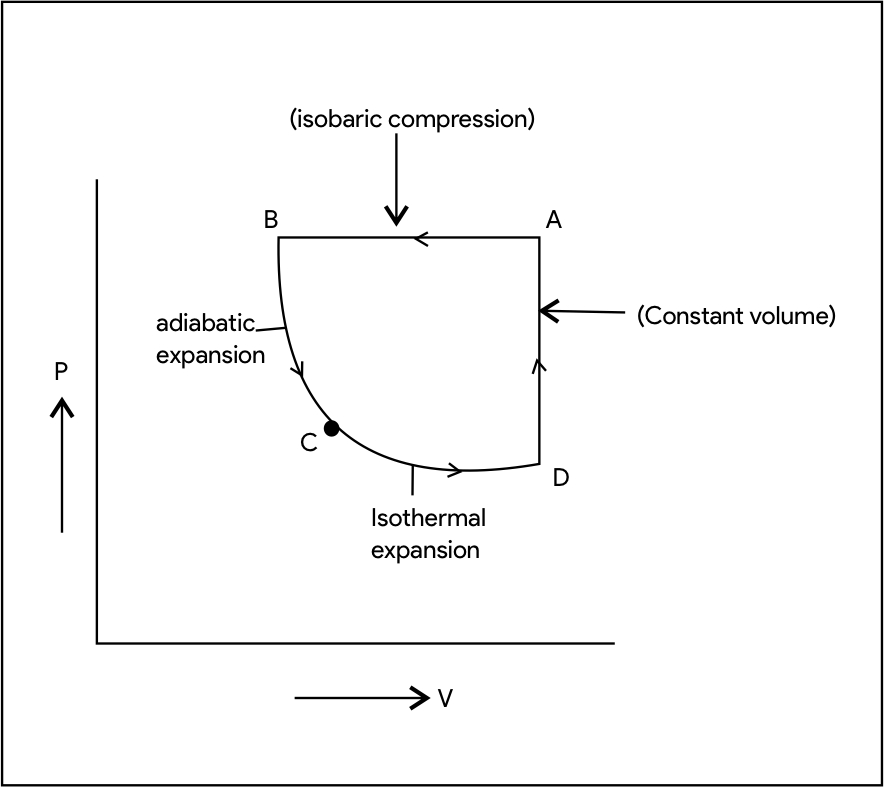
Help (4). Suppose we take n moles of a monatomic ideal gas through the following reversible cycle: AB is an isobariccompression; BC is an adiabatic expansion; CD is an isothermal expansion; DA is a constant volume pressureΔQincrease completing the cycle. (a) Show the cycle on a PV-diagram. (b) Express the heat flow, work Wchange in internal energyДЕthe change in entropyFint ,ASfor the legs AB, BC, and CD in terms of number ofmoles n, universal ideal gas constant R, 'ATA To., andTo

Answered: (4). Suppose we take n moles of a…

Elements Of Electromagnetics

7th Edition

ISBN:9780190698614

Author:Sadiku, Matthew N. O.

Publisher:Sadiku, Matthew N. O.

ChapterMA: Math Assessment

Section: Chapter Questions

Problem 1.1MA

See similar textbooks

Related questions

Concept explainers

Question

Help

(4). Suppose we take n moles of a monatomic ideal gas through the following reversible cycle: AB is an isobaric
compression; BC is an adiabatic expansion; CD is an isothermal expansion; DA is a constant volume pressure
ΔQ
increase completing the cycle. (a) Show the cycle on a PV-diagram. (b) Express the heat flow
, work W
change in internal energy
ДЕ
the change in entropy
Fint ,
AS
for the legs AB, BC, and CD in terms of number of
moles n, universal ideal gas constant R, 'A
TA To.
, and
To

Expert Solution

Step 1 P- V diagram

a) P-v diagram of given process:-

b) For isobaric process AB:-

$H e a t f l o w f r o m A T o B a s c o n s \tan t p r e s s u r e δ Q = n c_{p} d T δ Q = n c_{p} (T_{B} - T_{A}) δ Q = n \times \frac{γ R}{γ - 1} (T_{B} - T_{A}) w h e r e γ = a d i a b a t i c i n d e x f o r m o n o a t o m i c w h e r e c_{p} = s p e c i f i c h e a t c a p a c i t y a t c o n s \tan t p r e s s u r e f o r m o n o a t o m i c i d e a l g a s A n d W o r k δ W = P d v W_{1, 2} = P (v_{B} - V_{A}) W_{1, 2} = P V_{A} (\frac{V_{B}}{V_{A}} - 1) S i n c e P V = n R T S o \frac{V_{B}}{V_{A}} = \frac{T_{B}}{T_{A}} a n d P V_{A} = n R T_{A} W_{1, 2} = n R T_{A} (\frac{T_{B}}{T_{A}} - 1) N o w b y t h e r m o d y n a m i c s 1^{r s t} l a w δ Q = d E + δ W d E = δ Q - δ W d E = n \times \frac{γ R}{γ - 1} (T_{B} - T_{A}) - n R T_{A} (\frac{T_{B}}{T_{A}} - 1) O n s i m p l i f i c a t i o n d E = \frac{n R T_{A}}{γ - 1} (\frac{T_{B}}{T_{A}} - 1) A n d f r o m T - d s e q u a t i o n T d s = d h - v d p$

$T d s = n c_{p} d T - v d p d s = \frac{n γ R}{y - 1} \frac{d T}{T} - \frac{v}{T} d p \sin c e P V = n R T s o \frac{V}{T} = \frac{n R}{P} d s = \frac{n γ R}{y - 1} \frac{d T}{T} - \frac{n R}{P} d p o n i n t e g r a t e ∆ s = \frac{n γ R}{y - 1} \times \ln (\frac{T_{B}}{T_{A}}) - n R \ln (\frac{P_{B}}{P_{A}}) \sin c e p r o c e s s i s i s o b a r i c s o P_{A} = P_{B} ∆ s = \frac{n γ R}{y - 1} \times \ln (\frac{T_{B}}{T_{A}})$

Trending now

This is a popular solution!

Step by step

Solved in 3 steps with 1 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.

Similar questions