In this question, you will estimate the area under the curve y = 4x3 from x = 2 to x = 4 using three different Riemann sums. You will subdivide the interval [2,4] into four sub-intervals of equal width.
In this question, you will estimate the area under the curve
y = 4x3
from x = 2 to x = 4 using three different Riemann sums.
You will subdivide the interval [2,4] into four sub-intervals of equal width.
- Using our standard notation for Riemann sums, enter the values of a, b, n, and x.
a =
b =
n =
delta x =
- Complete the following table listing the four sub-intervals:
First subinterval : [ , ] Second subinterval : [ , ] Third subinterval : [ , ] Fourth subinterval : [ , ] - In the next two parts of the question, you will calculate the approximate area under the curve using the left end-points of the sub-intervals.
Complete the following table
x1 : f (x1) : x2 : f (x2) : x3 : f (x3) : x4 : f (x4) :
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

last follow up to this problem:
You can calculate the exact area under the curve using the Fundamental Theorem of Calculus:
(in image)
where F (x) is an antiderivative of the function f (x) = 4x3.
Find an antiderivative of the function f (x). Enter your constant of
Antiderivative :
Now find the exact value of the area under the curve.
Area =
Notice that your value of c does not matter when you calculate the area under the curve.
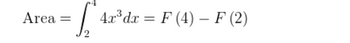
continuing off of that question:
4. In the next two parts of the question, you will calculate the approximate area under the curve using the right end-points of the sub-intervals.
Complete the following table (for the second column, you should only have to do one calculation from scratch, since you have already calculated three of the numbers earlier in the question).
| x1 | : | f (x1) | : |
| x2 | : | f (x2) | : |
| x3 | : | f (x3) | : |
| x4 | : | f (x4) | : |
5. Now calculate the approximate area under the curve using the formula
Approximate area under curve :
6.In the next two parts of the question, you will calculate the approximate area under the curve using the mid-points of the sub-intervals.
Complete the following table
| x1 | : | f (x1) | : |
| x2 | : | f (x2) | : |
| x3 | : | f (x3) | : |
| x4 | : | f (x4) | : |
7.Now calculate the approximate area under the curve using the formula
Approximate area under curve :








