4. a. Choose two points on the line shown here and use their coordinates to compute the slope of the line. b. Find an equation for the line. 2- -4 -2 4 6 -2- 4- 2.
4. a. Choose two points on the line shown here and use their coordinates to compute the slope of the line. b. Find an equation for the line. 2- -4 -2 4 6 -2- 4- 2.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**4.**
**a.** Choose two points on the line shown here and use their coordinates to compute the slope of the line.
**b.** Find an equation for the line.
---
**Graph Explanation:**
The graph is a coordinate plane with an x-axis and a y-axis intersecting at the origin (0,0). The axes are numbered from -6 to 6 on the x-axis and from -4 to 4 on the y-axis. A green line is drawn on the graph, rising diagonally from the bottom left to the top right.
- The line passes through points that can be visually estimated, such as (-4, -2) and (4, 3).
To calculate the slope (m) of the line, use the slope formula:
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
Substitute the chosen points:
\[ m = \frac{3 - (-2)}{4 - (-4)} = \frac{5}{8} \]
To find the equation of the line, use the slope-intercept form:
\[ y = mx + b \]
Use one of the points, say (-4, -2), to solve for b:
\[ -2 = \frac{5}{8}(-4) + b \]
\[ -2 = -\frac{20}{8} + b \]
\[ -2 = -2.5 + b \]
\[ b = 0.5 \]
Thus, the equation of the line is:
\[ y = \frac{5}{8}x + 0.5 \]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F78c21cba-5b52-4af3-891d-bb6502c9beeb%2F6d9e2e86-19df-430a-9245-9678969811f3%2Fgr2wb2e_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**4.**
**a.** Choose two points on the line shown here and use their coordinates to compute the slope of the line.
**b.** Find an equation for the line.
---
**Graph Explanation:**
The graph is a coordinate plane with an x-axis and a y-axis intersecting at the origin (0,0). The axes are numbered from -6 to 6 on the x-axis and from -4 to 4 on the y-axis. A green line is drawn on the graph, rising diagonally from the bottom left to the top right.
- The line passes through points that can be visually estimated, such as (-4, -2) and (4, 3).
To calculate the slope (m) of the line, use the slope formula:
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
Substitute the chosen points:
\[ m = \frac{3 - (-2)}{4 - (-4)} = \frac{5}{8} \]
To find the equation of the line, use the slope-intercept form:
\[ y = mx + b \]
Use one of the points, say (-4, -2), to solve for b:
\[ -2 = \frac{5}{8}(-4) + b \]
\[ -2 = -\frac{20}{8} + b \]
\[ -2 = -2.5 + b \]
\[ b = 0.5 \]
Thus, the equation of the line is:
\[ y = \frac{5}{8}x + 0.5 \]
Expert Solution
Step 1
Given that the graph
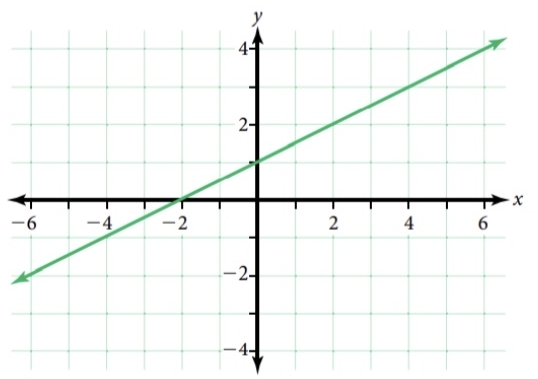
We have to first choose two point from the graph then find the equation of graph.
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

