4. A population's growth over time is modeled using the differential equation P'(t) = rP(t)(K – P(t)), where P(t) is the population at time t, and r and K are constants. (a) Show that this differential equation is separable. (b) Show that 1 1 1 P(t)(K – P(t)) KP(t) K(K – P(t))' (c) Use part (b) to find the general solution for this differential equation.
4. A population's growth over time is modeled using the differential equation P'(t) = rP(t)(K – P(t)), where P(t) is the population at time t, and r and K are constants. (a) Show that this differential equation is separable. (b) Show that 1 1 1 P(t)(K – P(t)) KP(t) K(K – P(t))' (c) Use part (b) to find the general solution for this differential equation.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Concept explainers
Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.
Topic Video
Question
stuck on part C

Transcribed Image Text:4. A population's growth over time is modeled using the differential equation
P'() — гP(t)(К — P()),
where P(t) is the population at time t, and r and K are constants.
(a) Show that this differential equation is separable.
(b) Show that
1
1
1
Р()(К — Р())
KP(t)
К (К — Р()*
(c) Use part (b) to find the general solution for this differential equation.
Expert Solution
Step 1
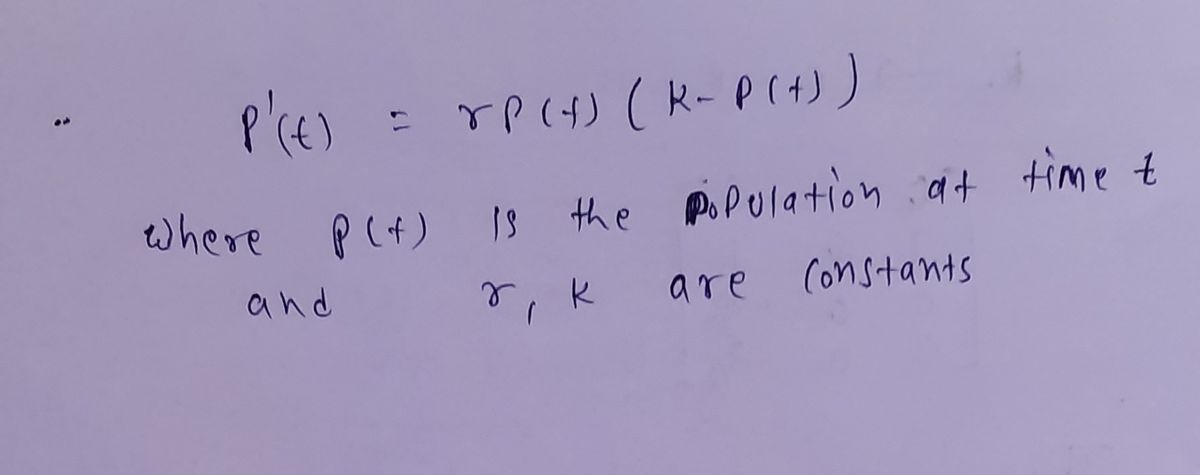
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

