4) Borus: Suppose one plate of a parallel-plate capacitor is tilted so it makes a small angle 0 with the other plate, as shown in Fig 24-28. Determine a formula for the capacitance C in terms of A, d, and 0 where A is the area of each plate and 0 is small. Assume the platles are square. [Hint Imagine the capacitor as many infinitesimal capacitors in parallel
4) Borus: Suppose one plate of a parallel-plate capacitor is tilted so it makes a small angle 0 with the other plate, as shown in Fig 24-28. Determine a formula for the capacitance C in terms of A, d, and 0 where A is the area of each plate and 0 is small. Assume the platles are square. [Hint Imagine the capacitor as many infinitesimal capacitors in parallel
Related questions
Question
100%
Please help and also provide components in the diagram.
![10:13 M J
LTE+
2l 77%|
9:41 P O
80%i
2022-02-17...
4/4
4) Bonus: Suppose one plate of a parallel-plate capacitor is tilted so it makes a small angle 0 with the other plate,
as shown in Fig. 24–28. Determine a formula for the capacitance C in terms of A, d, and 0 where A is the area of
each plate and O is small. Assume the plates are square. [Hint: Imagine the capacitor as many infinitesimal
capacitors in parallel]
EDIT
FILTERS
FORMAT](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff46f7989-8837-4e22-b5e6-5ecaa5af973e%2F3455de97-e389-4dc5-bdf0-9b3c02a2d870%2Fj0fyvs_processed.jpeg&w=3840&q=75)
Transcribed Image Text:10:13 M J
LTE+
2l 77%|
9:41 P O
80%i
2022-02-17...
4/4
4) Bonus: Suppose one plate of a parallel-plate capacitor is tilted so it makes a small angle 0 with the other plate,
as shown in Fig. 24–28. Determine a formula for the capacitance C in terms of A, d, and 0 where A is the area of
each plate and O is small. Assume the plates are square. [Hint: Imagine the capacitor as many infinitesimal
capacitors in parallel]
EDIT
FILTERS
FORMAT
Expert Solution
Step 1
Let the length of the plate be c. The area of the square plate is .
Consider a small length segment dx on the plate of the capacitor 'x' distance apart from its bottom.
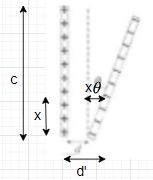
The capacitance of the finite small capacitor can be expressed as :
Step by step
Solved in 2 steps with 1 images
