Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question
![**Problem 13:**
**Task:** Solve the inequality and write the solution in interval notation.
\[
\frac{3x}{x-4} < 1
\]
**Solution Steps:**
1. **Subtract 1 from both sides:**
\[
\frac{3x}{x-4} - 1 < 0
\]
2. **Combine into a single fraction:**
\[
\frac{3x - (x - 4)}{x-4} < 0
\]
Simplify the numerator:
\[
\frac{3x - x + 4}{x-4} < 0
\]
\[
\frac{2x + 4}{x-4} < 0
\]
3. **Factor the expression:**
\[
\frac{2(x + 2)}{x-4} < 0
\]
4. **Find critical points:** Set the numerator and denominator equal to zero.
- Numerator: \(2(x + 2) = 0 \Rightarrow x = -2\)
- Denominator: \(x - 4 = 0 \Rightarrow x = 4\)
5. **Test intervals around critical points:**
Evaluate in intervals \((-\infty, -2)\), \((-2, 4)\), and \((4, \infty)\):
- Choose \(x = -3\) in \((-\infty, -2)\): \(\frac{2(-3 + 2)}{-3 - 4} = \frac{-2}{-7} > 0\)
- Choose \(x = 0\) in \((-2, 4)\): \(\frac{2(0 + 2)}{0 - 4} = \frac{4}{-4} < 0\)
- Choose \(x = 5\) in \((4, \infty)\): \(\frac{2(5 + 2)}{5 - 4} = \frac{14}{1} > 0\)
6. **Solution:** The solution in interval notation, where the inequality is negative, is \((-2, 4)\).
**Conclusion:** The solution to the inequality \(\frac{3](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Faa02accf-e7e0-450c-b255-e64057d9e798%2F81fcb62e-dab2-4acb-be1e-a4ac6f0fe9bf%2F12d8fde_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem 13:**
**Task:** Solve the inequality and write the solution in interval notation.
\[
\frac{3x}{x-4} < 1
\]
**Solution Steps:**
1. **Subtract 1 from both sides:**
\[
\frac{3x}{x-4} - 1 < 0
\]
2. **Combine into a single fraction:**
\[
\frac{3x - (x - 4)}{x-4} < 0
\]
Simplify the numerator:
\[
\frac{3x - x + 4}{x-4} < 0
\]
\[
\frac{2x + 4}{x-4} < 0
\]
3. **Factor the expression:**
\[
\frac{2(x + 2)}{x-4} < 0
\]
4. **Find critical points:** Set the numerator and denominator equal to zero.
- Numerator: \(2(x + 2) = 0 \Rightarrow x = -2\)
- Denominator: \(x - 4 = 0 \Rightarrow x = 4\)
5. **Test intervals around critical points:**
Evaluate in intervals \((-\infty, -2)\), \((-2, 4)\), and \((4, \infty)\):
- Choose \(x = -3\) in \((-\infty, -2)\): \(\frac{2(-3 + 2)}{-3 - 4} = \frac{-2}{-7} > 0\)
- Choose \(x = 0\) in \((-2, 4)\): \(\frac{2(0 + 2)}{0 - 4} = \frac{4}{-4} < 0\)
- Choose \(x = 5\) in \((4, \infty)\): \(\frac{2(5 + 2)}{5 - 4} = \frac{14}{1} > 0\)
6. **Solution:** The solution in interval notation, where the inequality is negative, is \((-2, 4)\).
**Conclusion:** The solution to the inequality \(\frac{3
Expert Solution
Step 1
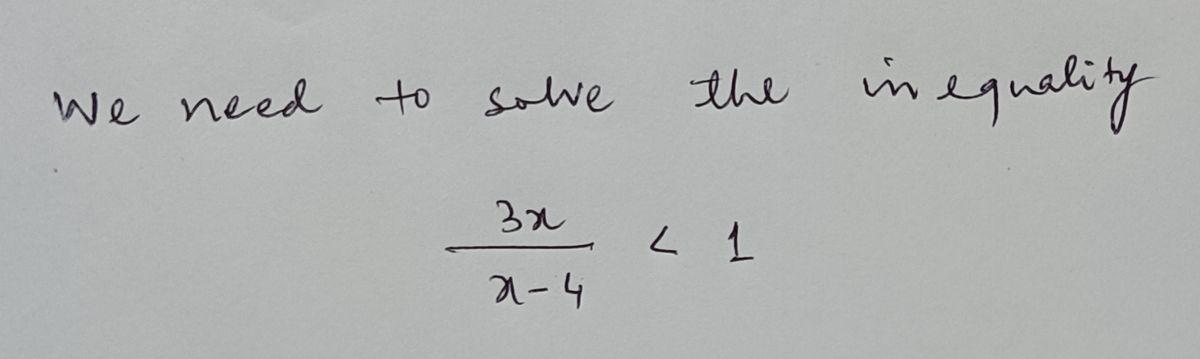
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education