Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
3d
![9:26 MEI ✔
C
(d)
(e)
(c)
(1) + ² ( 2 ) + ³ ( 3 ) + ··· + n(") = n2²−¹.
3
n2n-1
(f)
(b)
(6) + (0+3)
(c)
5
each of the identities al 28%
[Hint: Let a = b = 1 in the binomial theorem.]
-- + (−1)" ("")
[Hint: After expanding n(1 + b)"-1 by the binomial theore
that
(0) + ² (7) + ²² (²)
(8) + (2) + (4) + (3)
(1) + (3) + (3)
=
4. Prove the following for n ≥ 1:
n (" z ¹)
k
[Hint: Use parts (a) and (b).]
1
(0) − ½ (01) + ½ (2) -
-
3
[Hint: The left-hand side equals
1
|||
5. (a)en 22, pe that
+... + 2"
= (k+1)
+...
O
„+₁[("†')-("+¹)+("‡¹) ---
2
n
¹)(1+1).J
k+
(3)
24 of 450
+ ... = 2n-1.
(-1)"
n+1
n
1
(a)
(") <(₁ + ₁) if and only if 0 < r < (n − 1).
r+1
n
1)
if and only if n - 1 ≥ r > −(n − 1).
(n-1
r+1
(7) > ( , + ₁)
(7) - (, 4₁)
n
=
= 3".
(1)=+++
n
0
3
if and only if n is an odd integer, and r =
+(-
:](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fee3fd376-1486-4f61-9700-b2f5e0311640%2F2b1b2428-cf18-45c6-87bc-f0c3d04be09c%2Fyptdz5j_processed.jpeg&w=3840&q=75)
Transcribed Image Text:9:26 MEI ✔
C
(d)
(e)
(c)
(1) + ² ( 2 ) + ³ ( 3 ) + ··· + n(") = n2²−¹.
3
n2n-1
(f)
(b)
(6) + (0+3)
(c)
5
each of the identities al 28%
[Hint: Let a = b = 1 in the binomial theorem.]
-- + (−1)" ("")
[Hint: After expanding n(1 + b)"-1 by the binomial theore
that
(0) + ² (7) + ²² (²)
(8) + (2) + (4) + (3)
(1) + (3) + (3)
=
4. Prove the following for n ≥ 1:
n (" z ¹)
k
[Hint: Use parts (a) and (b).]
1
(0) − ½ (01) + ½ (2) -
-
3
[Hint: The left-hand side equals
1
|||
5. (a)en 22, pe that
+... + 2"
= (k+1)
+...
O
„+₁[("†')-("+¹)+("‡¹) ---
2
n
¹)(1+1).J
k+
(3)
24 of 450
+ ... = 2n-1.
(-1)"
n+1
n
1
(a)
(") <(₁ + ₁) if and only if 0 < r < (n − 1).
r+1
n
1)
if and only if n - 1 ≥ r > −(n − 1).
(n-1
r+1
(7) > ( , + ₁)
(7) - (, 4₁)
n
=
= 3".
(1)=+++
n
0
3
if and only if n is an odd integer, and r =
+(-
:
Expert Solution
Step 1
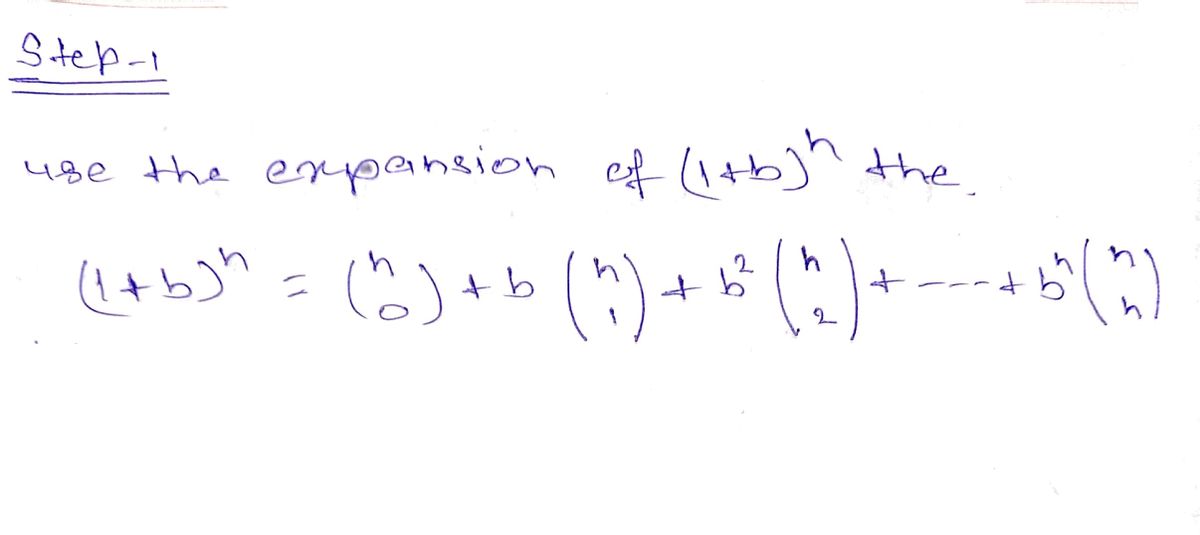
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

