3a. Let f,g: ACR → R and c E A'. Assume that there is a 6> 0 such that f (x) = g(x) for all x € A such that 0 < x − c < 6. Show that if lim f (x) exist then limg (x) exists and x-c x-c lim f (x) x-c = limg(x). Argue that lim g(x) exists and x-c x-c In other words, lim f (x) depends only on the values of f (x) for x near c- this fact is often expressed by saying that limits are a "local property". x→a Notice that if lim f (x) = L exists then for € > 0, there is 0 < 6₁ ≤ 6, such that, for all x € A, if 0< x- c < 6₁, then f (x) - L < €. x-c Show that, for all x € A, if 0 < |x − c < 8₁, then [g (x) − L| < €. lim f (x) = limg(x). x-c x-C Explain the meaning of the expression that limits are a "local property".
3a. Let f,g: ACR → R and c E A'. Assume that there is a 6> 0 such that f (x) = g(x) for all x € A such that 0 < x − c < 6. Show that if lim f (x) exist then limg (x) exists and x-c x-c lim f (x) x-c = limg(x). Argue that lim g(x) exists and x-c x-c In other words, lim f (x) depends only on the values of f (x) for x near c- this fact is often expressed by saying that limits are a "local property". x→a Notice that if lim f (x) = L exists then for € > 0, there is 0 < 6₁ ≤ 6, such that, for all x € A, if 0< x- c < 6₁, then f (x) - L < €. x-c Show that, for all x € A, if 0 < |x − c < 8₁, then [g (x) − L| < €. lim f (x) = limg(x). x-c x-C Explain the meaning of the expression that limits are a "local property".
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please answer all parts. and include the picture of your solution. Thanks
![3a. Let \( f, g : A \subseteq \mathbb{R} \rightarrow \mathbb{R} \) and \( c \in A' \). Assume that there is a \( \delta > 0 \) such that \( f(x) = g(x) \) for all \( x \in A \) such that \( 0 < |x - c| < \delta \). Show that if \( \lim_{x \to c} f(x) \) exists then \( \lim_{x \to c} g(x) \) exists and
\[
\lim_{x \to c} f(x) = \lim_{x \to c} g(x).
\]
In other words, \( \lim_{x \to c} f(x) \) depends only on the values of \( f(x) \) for \( x \) near \( c \) – this fact is often expressed by saying that limits are a "local property".
Notice that if \( \lim_{x \to c} f(x) = L \) exists then for \( \varepsilon > 0 \), there is \( 0 < \delta_1 \leq \delta \), such that, for all \( x \in A \), if \( 0 < |x - c| < \delta_1 \), then \( |f(x) - L| < \varepsilon \).
- Show that, for all \( x \in A \), if \( 0 < |x - c| < \delta_1 \), then \( |g(x) - L| < \varepsilon \).
- Argue that \( \lim_{x \to c} g(x) \) exists and
\[
\lim_{x \to c} f(x) = \lim_{x \to c} g(x).
\]
- Explain the meaning of the expression that limits are a "local property".](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fa8d46346-fe9f-45aa-a3a0-df12b7cae379%2Ff5b4d590-b98b-4146-8662-e56598ef9cac%2Fn1d9bhh_processed.png&w=3840&q=75)
Transcribed Image Text:3a. Let \( f, g : A \subseteq \mathbb{R} \rightarrow \mathbb{R} \) and \( c \in A' \). Assume that there is a \( \delta > 0 \) such that \( f(x) = g(x) \) for all \( x \in A \) such that \( 0 < |x - c| < \delta \). Show that if \( \lim_{x \to c} f(x) \) exists then \( \lim_{x \to c} g(x) \) exists and
\[
\lim_{x \to c} f(x) = \lim_{x \to c} g(x).
\]
In other words, \( \lim_{x \to c} f(x) \) depends only on the values of \( f(x) \) for \( x \) near \( c \) – this fact is often expressed by saying that limits are a "local property".
Notice that if \( \lim_{x \to c} f(x) = L \) exists then for \( \varepsilon > 0 \), there is \( 0 < \delta_1 \leq \delta \), such that, for all \( x \in A \), if \( 0 < |x - c| < \delta_1 \), then \( |f(x) - L| < \varepsilon \).
- Show that, for all \( x \in A \), if \( 0 < |x - c| < \delta_1 \), then \( |g(x) - L| < \varepsilon \).
- Argue that \( \lim_{x \to c} g(x) \) exists and
\[
\lim_{x \to c} f(x) = \lim_{x \to c} g(x).
\]
- Explain the meaning of the expression that limits are a "local property".
Expert Solution
Step 1: Explanation - 1
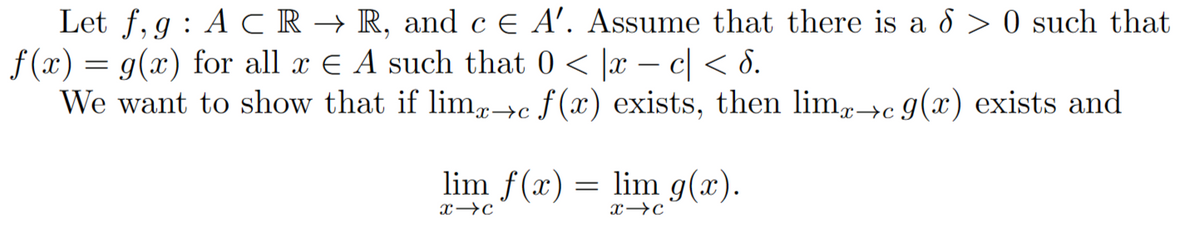
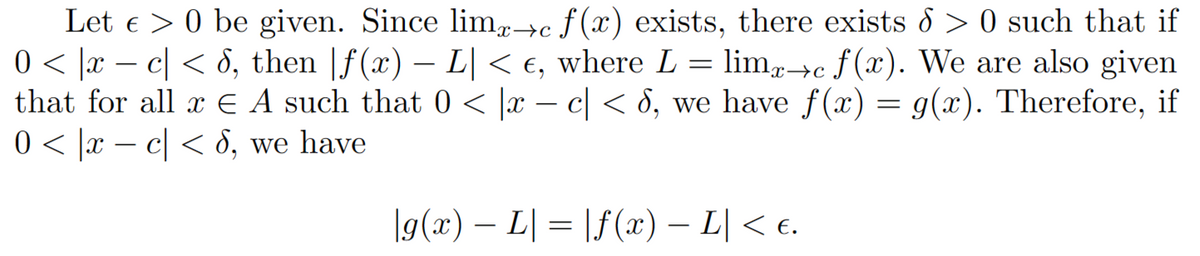
Step by step
Solved in 3 steps with 5 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

