Homework Help is Here – Start Your Trial Now!
Math
Calculus
35. у 3 х -2

35. у 3 х -2

Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
See similar textbooks
icon
Related questions
Question
**Task 34–35:** Use a graphing calculator or computer to graph both the curve and its curvature function \( \kappa(x) \) on the same screen. Is the graph of \( \kappa \) what you would expect? **Explanation:** This task involves plotting two graphs on the same screen using a graphing calculator or computer software. The first graph is the curve itself, and the second is its curvature function \( \kappa(x) \). The curvature function describes how the curve changes direction at any given point. By comparing these two graphs, students can analyze the relationship between the curve and its curvature. The question encourages reflection on expectations regarding the form and behavior of the curvature graph.
Transcribed Image Text:**Task 34–35:** Use a graphing calculator or computer to graph both the curve and its curvature function \( \kappa(x) \) on the same screen. Is the graph of \( \kappa \) what you would expect? **Explanation:** This task involves plotting two graphs on the same screen using a graphing calculator or computer software. The first graph is the curve itself, and the second is its curvature function \( \kappa(x) \). The curvature function describes how the curve changes direction at any given point. By comparing these two graphs, students can analyze the relationship between the curve and its curvature. The question encourages reflection on expectations regarding the form and behavior of the curvature graph.
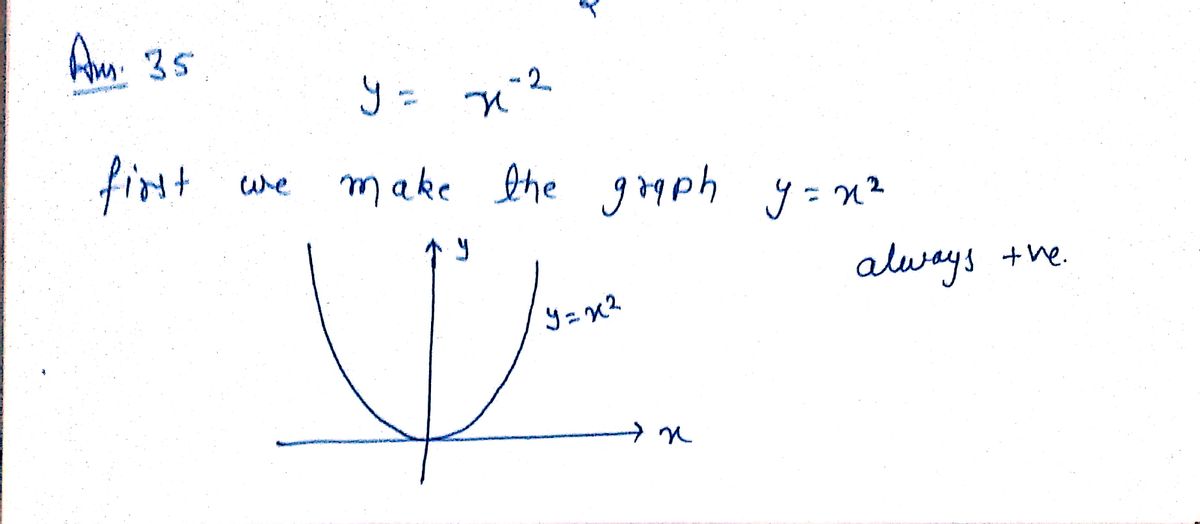
**Equation 35: Rational Function** The equation is given by: \[ y = x^{-2} \] ### Explanation: This represents a rational function where \( y \) is equal to the reciprocal of \( x \) squared. The function can also be written as: \[ y = \frac{1}{x^2} \] ### Characteristics: 1. **Domain:** The function is defined for all \( x \) except \( x = 0 \). This means \( x \) cannot be zero because division by zero is undefined. 2. **Range:** \( y > 0 \) for all \( x \neq 0 \). The values of \( y \) are positive because squaring \( x \) and taking its reciprocal always results in a positive value. 3. **Asymptotes:** - **Vertical Asymptote:** At \( x = 0 \), the function approaches infinity. - **Horizontal Asymptote:** As \( x \) approaches infinity or negative infinity, \( y \) approaches 0. ### Graph Interpretation: The graph of this function is a curve in the first and second quadrants of the Cartesian plane. It approaches the x-axis (horizontal asymptote) but never touches it, and it rises steeply as it approaches the y-axis from either side.
Transcribed Image Text:**Equation 35: Rational Function** The equation is given by: \[ y = x^{-2} \] ### Explanation: This represents a rational function where \( y \) is equal to the reciprocal of \( x \) squared. The function can also be written as: \[ y = \frac{1}{x^2} \] ### Characteristics: 1. **Domain:** The function is defined for all \( x \) except \( x = 0 \). This means \( x \) cannot be zero because division by zero is undefined. 2. **Range:** \( y > 0 \) for all \( x \neq 0 \). The values of \( y \) are positive because squaring \( x \) and taking its reciprocal always results in a positive value. 3. **Asymptotes:** - **Vertical Asymptote:** At \( x = 0 \), the function approaches infinity. - **Horizontal Asymptote:** As \( x \) approaches infinity or negative infinity, \( y \) approaches 0. ### Graph Interpretation: The graph of this function is a curve in the first and second quadrants of the Cartesian plane. It approaches the x-axis (horizontal asymptote) but never touches it, and it rises steeply as it approaches the y-axis from either side.
Expert Solution
Step 1

Calculus homework question answer, step 1, image 1

trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Knowledge Booster
Research Ethics
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Precalculus
Precalculus
Calculus
ISBN:
9780135189405
Author:
Michael Sullivan
Publisher:
PEARSON
Calculus: Early Transcendental Functions
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS