341 and 3640 How many bits are required to store this number?explain How do you find it and show your works.
341 and 3640 How many bits are required to store this number?explain How do you find it and show your works.
Integers are stored in using the word memory. This word is equal to 4 bytes or 32 bits.
So, the integers from 0 to can be stored using these 4 bytes or 32 bits memory.
Example:
Integer 1 is expressed as a 32-bit value
1: 00000001 00000000 00000000 00000000
ISSUES:
There are two issues for the above rule,
This does not fit
- for negative numbers
- for very large numbers 2^32 or greater. These large valued numbers cannot be stored in 32-bit of memory.
SOLUTION:
1) In the case of negative numbers, we can clear this issue by sacrificing one bit as the Sign bit to indicate whether it is negative or positive.
- 1 indicates a negative number
- 0 indicates a positive number.
Thus, the integers range from to .
2) In the case of very large integers, we need to use more memory to store the large value, such as two words per integer.
NOTE:
A word is represented as a collection of 32-bits or a collection of 4-bytes.
1) 341
convert 341 to binary value.
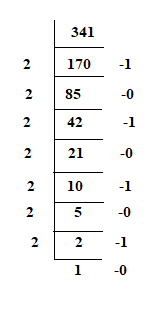
so,
thus, the number 341 can be represented as a 32-bit value as follows,
10101010 10000000 00000000 00000000
ANSWER:
This number 341 can be stored using 32-bits of memory.
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 2 images









