**Problem 33:** Find the points of intersection between the line $ x - y - 2 = 0 $ and the parabola $ y = 4 - x^2 $.**Solution:**To find the points of intersection, we need to solve the two equations simultaneously.Firstly, solve the linear equation for $ y $:\[ x - y - 2 = 0 \]\[ y = x - 2 \]Now, substitute $ y = x - 2 $ into the equation of the parabola:\[ y = 4 - x^2 \]\[ x - 2 = 4 - x^2 \]Rearrange to form a quadratic equation:\[ x^2 + x - 6 = 0 \]Next, solve the quadratic equation $ x^2 + x - 6 = 0 $ using the quadratic formula, factoring, or completing the square.Assuming factoring is possible:\[ (x + 3)(x - 2) = 0 \]Thus, the solutions are:\[ x = -3 \quad \text{or} \quad x = 2 \]Substitute these $ x $ values back into the linear equation to find the corresponding $ y $ values.For $ x = -3 $:\[ y = -3 - 2 = -5 \]Thus, one point of intersection is $ (-3, -5) $.For $ x = 2 $:\[ y = 2 - 2 = 0 \]Thus, the other point of intersection is $ (2, 0) $.**Conclusion:**The points of intersection between the line and the parabola are $ (-3, -5) $ and $ (2, 0) $.

Answered: Image /qna-images/answer/fb9e5b80-2f71-487d-b2f1-7f9eb562f99c.jpg

Answered: 33) Find the points of intersection…

Math

Geometry

33) Find the points of intersection between the line x - y - 2 = 0 and the parabola y = 4 - x 2.

Elementary Geometry For College Students, 7e

7th Edition

ISBN:9781337614085

Author:Alexander, Daniel C.; Koeberlein, Geralyn M.

Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.

ChapterP: Preliminary Concepts

SectionP.CT: Test

Problem 1CT

See similar textbooks

Related questions

Q: Nhat is the equation of the parabola containing the points (2, 2), (4,-8), and (-2, –14)? O y = - 4x…

Q: What is the vertex of the parabola y=(x+3)²-4? A (3,4) B (-3,4)

A: The vertex of standard parabola equation y = x2 is at (0,0)

Q: There is a parabola which has a minimum where the two lines 3x+6y-1=0 and 2x+ y-2=0 intersect. The…

Q: Q4) Find the y-intercept, x-intercept(s) and the vertex point for the parabola y = x2 + 6x + 5 then…

A: Given: Parabola: y=x2+6x+5 To Find: The y-intercept, x-intercepts and the vertex point for the…

Q: What is the equation of the parabola containing the points (0, 5), (–1,9), and (2, 3)? O y = r-z+5 O…

A: The standard form of a parabola is y=ax2+bx+c. The required parabola passes through the 3 points are…

Q: FIND THE VERTEX USING X=-B/2A, THEN USE TABLE OF VALUES AND FIND 4 OTHER POINTS FOR A PARABOLA…

A: (a) y=x2+2x-4 We know that the vertex of the parabola y=ax2+bx+c is -b2a,y Therefore comparing the…

Q: 91 a) Find an equation of the sphere with center (1,-3,-5) and tangent to xz-plane.

Q: Find the area of the right triangle with vertices J(6, 5), K(1, 7), and L(2, −5).

A: We know that the area of the right angle triangle is 1/2*base*height

Q: Arrange the parabolas represented by the equations according to the positions of their foci on the…

A: The standard form of a parabola is (x – h)2 = a(y – k) where (h, k) is the vertex.

Concept explainers

Maximization

Have you ever seen a bridge in the shape of a parabola? Where is its maximum on the bridge? The maximum of that bridge is the highest point on that bridge. The process of finding the maximum of the bridge here is called the maximization.

Question

**Problem 33:** Find the points of intersection between the line $ x - y - 2 = 0 $ and the parabola $ y = 4 - x^2 $.

**Solution:**

To find the points of intersection, we need to solve the two equations simultaneously.

Firstly, solve the linear equation for $ y $:
\[ x - y - 2 = 0 \]
\[ y = x - 2 \]

Now, substitute $ y = x - 2 $ into the equation of the parabola:
\[ y = 4 - x^2 \]
\[ x - 2 = 4 - x^2 \]

Rearrange to form a quadratic equation:
\[ x^2 + x - 6 = 0 \]

Next, solve the quadratic equation $ x^2 + x - 6 = 0 $ using the quadratic formula, factoring, or completing the square.

Assuming factoring is possible:
\[ (x + 3)(x - 2) = 0 \]

Thus, the solutions are:
\[ x = -3 \quad \text{or} \quad x = 2 \]

Substitute these $ x $ values back into the linear equation to find the corresponding $ y $ values.

For $ x = -3 $:
\[ y = -3 - 2 = -5 \]
Thus, one point of intersection is $ (-3, -5) $.

For $ x = 2 $:
\[ y = 2 - 2 = 0 \]
Thus, the other point of intersection is $ (2, 0) $.

**Conclusion:**

The points of intersection between the line and the parabola are $ (-3, -5) $ and $ (2, 0) $.

Expert Solution

Drawing rough view and solving equation

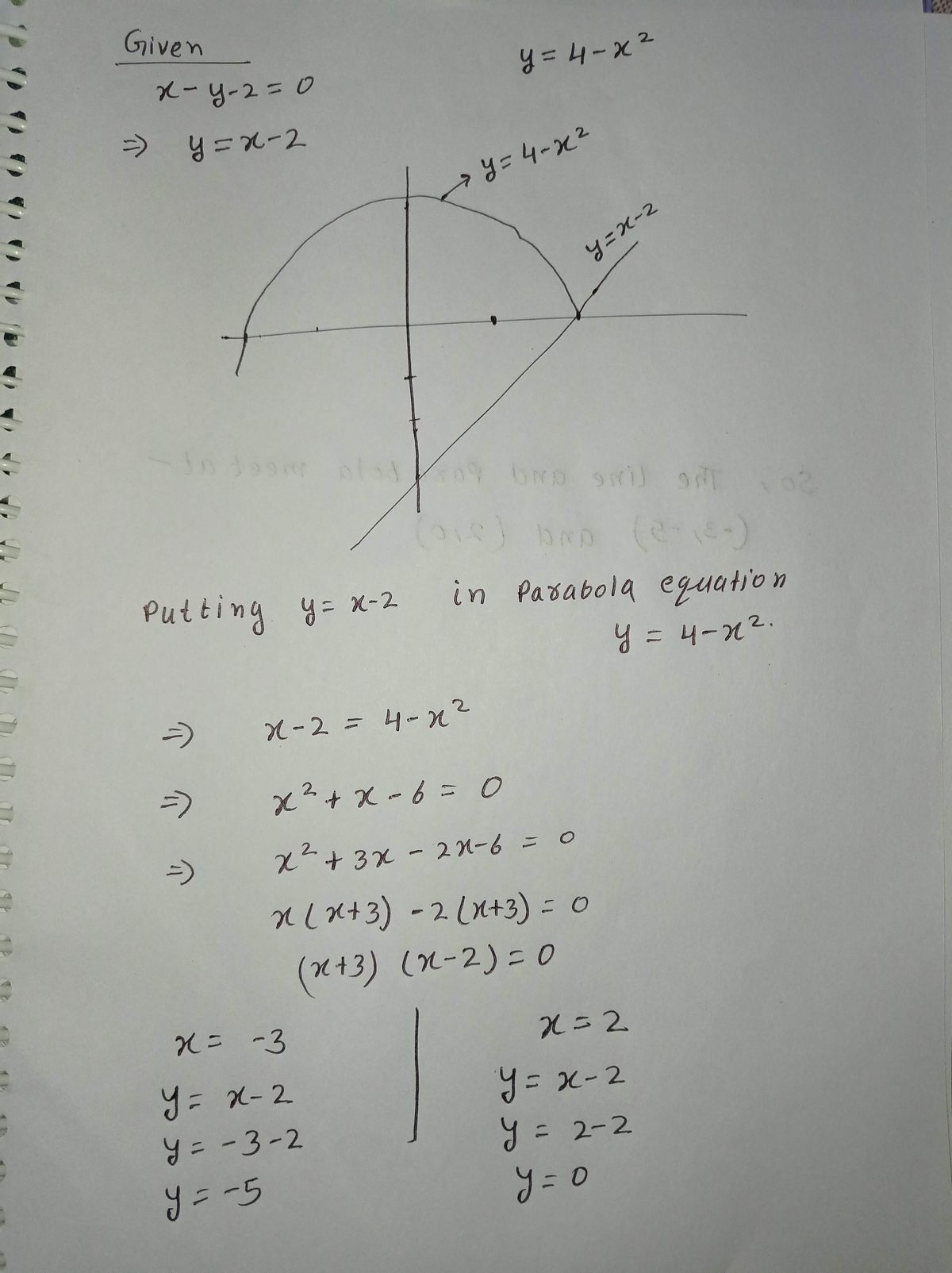
Step by step

Solved in 2 steps with 2 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Parabolas$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.

Similar questions

What are the coordinates where the parabola intersects the line? Show all work in a clear, easy to read format. Use algebra to solve any equations. Give answers accurate to the nearest thousandth. (-1, 0) (5, 0) 8. (6, -8.5) |(-1, –19) (1, –19.6) Line: y=1.5x-17.5 -20- 49x2 y = 49х 49 Parabola: 20 5 4
Q,9. What point on the parabola y = v2x + 5 comes closest to the origin.
7. Write an equation for each parabola. a) (0, 11) 4 (4, –5) b) YA (-6, 4) 4 (-5,3) -6 -2 0 x c) YA 12 (4,13) 14 +4 (6, –7) -c
3
6) Find the equation of a parabola containing points any method: 16), (-3, -0.5), (0, -5) (-6,