3. Using Mason's Rule, find the transfer function T(s) = for the system represented in the fugre. C(s) R(s) G₁(s) G₂(s) G4(S) G7(s) R(s) G3(s) G5(s) G6(s) H₁(s) Hz(s) H₂(s) C(s)
Follow the instructions. Kindly provide a COMPLETE and CLEAR solution. Answer it ASAP because I really need it right now. Answer should be typewritten.
Provide the following:
Step 1. Solve for k
Step 2. Solve for Tk (forward path gain)
Step 3. Identify the loop gains (TL)
Step 4. Identify the nontouching loops taken two at a time TNL(2 time)
Step 5. Identify the nontouching loops taken three at a time TNL(3 time)
Step 6. Identify the nontouching loops taken four at a time TNL(4 time)
Step 7. Solve for component ∆
Step 8. Solve for component ∆k (Note: We form ∆k by eliminating from ∆ the loop gains that touch the kth forward path)
Step 9. Substitute on the equation for transfer function

Step by step
Solved in 11 steps with 11 images

Follow the instructions. Kindly provide a COMPLETE and CLEAR solution. Answer it ASAP because I really need it right now.
Answer should be typewritten.
Provide the following:
Step 1. Solve for k
Step 2. Solve for Tk (forward path gain)
Step 3. Identify the loop gains (TL)
Step 4. Identify the nontouching loops taken two at a time TNL(2 time)
Step 5. Identify the nontouching loops taken three at a time TNL(3 time)
Step 6. Identify the nontouching loops taken four at a time TNL(4 time)
Step 7. Solve for component ∆
Step 8. Solve for component ∆k (Note: We form ∆k by eliminating from ∆ the loop gains that touch the kth forward path)
Step 9. Substitute on the equation for transfer function
Formula:
∆ = 1- ΣTCL + ΣTNL(2 time) - ΣTNL(3 time)+ ΣTNL(4 time)+ ......
∆k = ∆ - ΣTL touch kth forward path
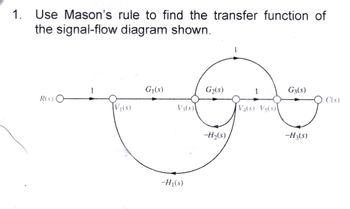
Can you redo Step 7. Solve for component ∆, Step 8. Solve for component ∆k , and Step 9. Substitute on the equation for transfer function. (Transfer function is given in the photo below, kindly provide the solution how the answer to the transfer function became like that.)
Here is the formula:
∆ = 1- ΣTCL + ΣTNL(2 time) - ΣTNL(3 time)+ ΣTNL(4 time)+ ......
∆k = ∆ - ΣTL touch kth forward path









