3. Use the definition of a convex set to show that if S₁ and S₂ are convex sets in R+", then so is their partial sum S = {(x,y₁ + y₂) | ER",3₁,32 € R"; (a; y₁) € S₁, (x, y2) € S₂}.
3. Use the definition of a convex set to show that if S₁ and S₂ are convex sets in R+", then so is their partial sum S = {(x,y₁ + y₂) | ER",3₁,32 € R"; (a; y₁) € S₁, (x, y2) € S₂}.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Topic: Convex Sets and Partial Sums**
Use the definition of a convex set to show that if \( S_1 \) and \( S_2 \) are convex sets in \( \mathbb{R}^{m+n} \), then so is their partial sum:
\[
S = \{ (x, y_1 + y_2) \mid x \in \mathbb{R}^m, y_1, y_2 \in \mathbb{R}^n; (x, y_1) \in S_1, (x, y_2) \in S_2 \}.
\]
**Explanation:**
This problem explores the properties of convex sets—specifically, demonstrating that a certain construction of two convex sets results in another convex set. The sets \( S_1 \) and \( S_2 \) are given as convex in a higher-dimensional space \( \mathbb{R}^{m+n} \).
The task is to show that the set \( S \), formed by taking elements \( x \) from \( \mathbb{R}^m \) and summing elements \( y_1 \) and \( y_2 \) from \( \mathbb{R}^n \) such that \( (x, y_1) \in S_1 \) and \( (x, y_2) \in S_2 \), retains the convex property.
**Approach Required:**
To demonstrate the convexity of \( S \), one must use the definition of convexity, which involves showing that for any two points in \( S \), any convex combination (a linear combination where the coefficients sum to 1 and are non-negative) of these points is also in \( S \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff4589616-f4fd-4eb5-854c-a0440b9d838b%2F06798b6f-b9c0-4fde-99ab-9256d6871410%2Fwnnaheq_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Topic: Convex Sets and Partial Sums**
Use the definition of a convex set to show that if \( S_1 \) and \( S_2 \) are convex sets in \( \mathbb{R}^{m+n} \), then so is their partial sum:
\[
S = \{ (x, y_1 + y_2) \mid x \in \mathbb{R}^m, y_1, y_2 \in \mathbb{R}^n; (x, y_1) \in S_1, (x, y_2) \in S_2 \}.
\]
**Explanation:**
This problem explores the properties of convex sets—specifically, demonstrating that a certain construction of two convex sets results in another convex set. The sets \( S_1 \) and \( S_2 \) are given as convex in a higher-dimensional space \( \mathbb{R}^{m+n} \).
The task is to show that the set \( S \), formed by taking elements \( x \) from \( \mathbb{R}^m \) and summing elements \( y_1 \) and \( y_2 \) from \( \mathbb{R}^n \) such that \( (x, y_1) \in S_1 \) and \( (x, y_2) \in S_2 \), retains the convex property.
**Approach Required:**
To demonstrate the convexity of \( S \), one must use the definition of convexity, which involves showing that for any two points in \( S \), any convex combination (a linear combination where the coefficients sum to 1 and are non-negative) of these points is also in \( S \).
Expert Solution
Step 1: Concept of a convex set
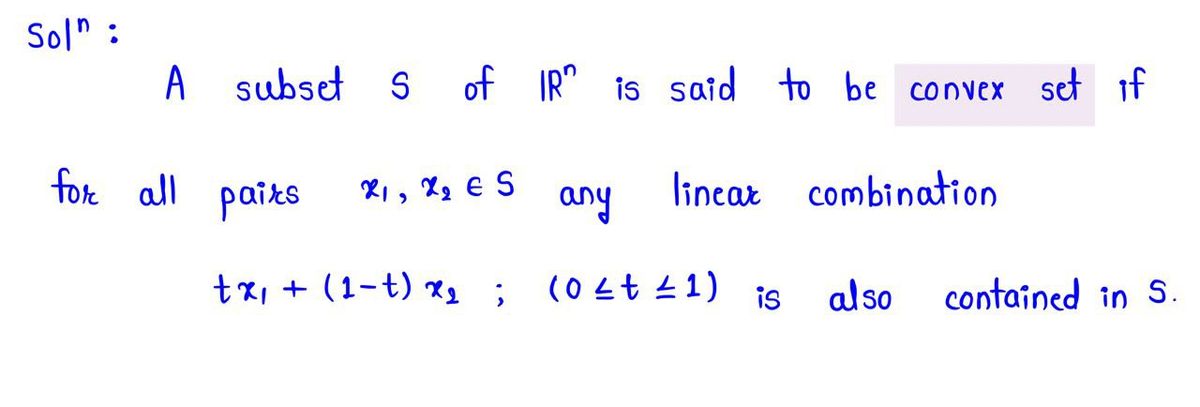
Step by step
Solved in 4 steps with 4 images

Similar questions
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

