3. Given the function f(x) = -log₂ (x + 1)-2. Do the following. a) Determine the parent function and sketch its graph. -10 -8 -6 b) Find the x-intercept of f(x). c) Find the y-intercept of f(x). -4 y -2 10 8 6 4 2 -2 -4 -6 -8 -10 2 d) Is there a vertical asymptote? If so, what is it? e) Is there a horizontal asymptote? If so, what is it? 4 6 8 10 X
3. Given the function f(x) = -log₂ (x + 1)-2. Do the following. a) Determine the parent function and sketch its graph. -10 -8 -6 b) Find the x-intercept of f(x). c) Find the y-intercept of f(x). -4 y -2 10 8 6 4 2 -2 -4 -6 -8 -10 2 d) Is there a vertical asymptote? If so, what is it? e) Is there a horizontal asymptote? If so, what is it? 4 6 8 10 X
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question

Transcribed Image Text:### Exercise: Logarithmic Function Analysis
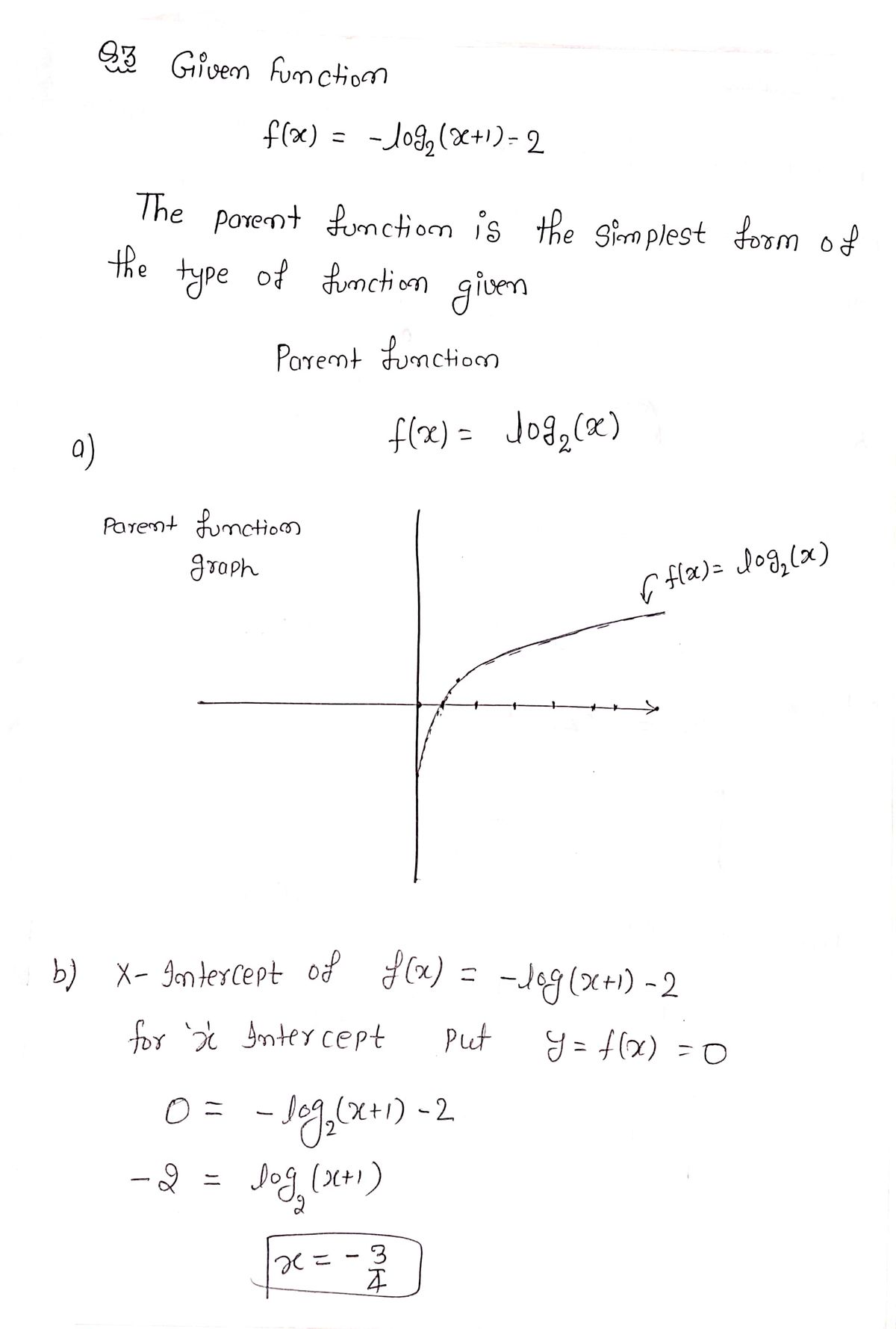
Given the function \( f(x) = -\log_2(x + 1) - 2 \), complete the following tasks:
#### a) Determine the parent function and sketch its graph.
Parent Function: The parent function of \( f(x) = -\log_2(x + 1) - 2 \) is \( \log_2(x) \).
- **Graph Explanation:**
- The graph is a standard Cartesian coordinate system with the x-axis labeled from -10 to 10 and the y-axis labeled from -10 to 10.
- The scale is uniform, with grid lines at every unit on both axes.
- The graph should depict a transformation of the logarithmic function, involving reflection over the x-axis, a shift to the left by 1 unit, and a downward shift by 2 units.
#### b) Find the x-intercept of \( f(x) \).
- **X-Intercept:** Solve \( f(x) = 0 \) to find \( x \).
#### c) Find the y-intercept of \( f(x) \).
- **Y-Intercept:** Evaluate \( f(0) \).
#### d) Is there a vertical asymptote? If so, what is it?
- **Vertical Asymptote:** There is a vertical asymptote at \( x = -1 \) due to the transformation \( (x + 1) \).
#### e) Is there a horizontal asymptote? If so, what is it?
- **Horizontal Asymptote:** Analyze the function as \( x \to \infty \).
Note that each task should be completed with detailed calculations and graphing as needed to facilitate understanding.

Transcribed Image Text:**Educational Website Content:**
### Exercise on Function and Graph Analysis
#### Part f: Sketching the Graph of \( f(x) \)
- **Task**: Sketch the graph of \( f(x) \). Make sure to label all intercepts and asymptotes.
- **Graph Details**:
- The graph is plotted on a standard coordinate plane.
- The x-axis and y-axis are labeled from -10 to 10.
- Each axis is divided into increments of 2.
- **Instructions**:
1. Identify and label the x-intercepts and y-intercepts on the graph.
2. Determine any vertical or horizontal asymptotes and mark them clearly.
#### Part g: Analyzing Domain and Range
- **Task**: Find the domain and range of \( f(x) \).
- **Instructions**:
1. Determine the set of all possible x-values (domain) for which the function \( f(x) \) is defined.
2. Identify the set of all possible y-values (range) that the function can take.
### Tips for Solution:
- Review the characteristics of the function \( f(x) \) to determine intercepts and asymptotes.
- Use the graph to visually verify the intercepts and asymptotic behavior.
- Apply the definition of domain and range in the context of the graph and the function's equation (if provided).
Use these guidelines to complete the exercise and deepen your understanding of graphing functions and analyzing their properties.
Expert Solution
Step 1
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning