Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
3. 4. sin n √n √√n² + 2 n² + n-n

3. 4. sin n √n √√n² + 2 n² + n-n

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question

Hello there, can you help me solve problems? Thanks!

Determine whether the given limits exist and find their values. Give a clear explanation.

 

### Mathematical Expressions 3. \(\frac{\sin n}{\sqrt{n}}\) This expression represents a quotient where the sine of \(n\) is divided by the square root of \(n\). It involves trigonometric and radical functions. 4. \(\sqrt{n^2 + n - n}\) This expression is a radical expression that simplifies to \(\sqrt{n^2}\) because the terms \(+n\) and \(-n\) cancel each other out. The final form is the square root of \(n^2\), which simplifies to \(n\), assuming \(n\) is non-negative.
Transcribed Image Text:### Mathematical Expressions 3. \(\frac{\sin n}{\sqrt{n}}\) This expression represents a quotient where the sine of \(n\) is divided by the square root of \(n\). It involves trigonometric and radical functions. 4. \(\sqrt{n^2 + n - n}\) This expression is a radical expression that simplifies to \(\sqrt{n^2}\) because the terms \(+n\) and \(-n\) cancel each other out. The final form is the square root of \(n^2\), which simplifies to \(n\), assuming \(n\) is non-negative.
Expert Solution
Step 1: Question 3:

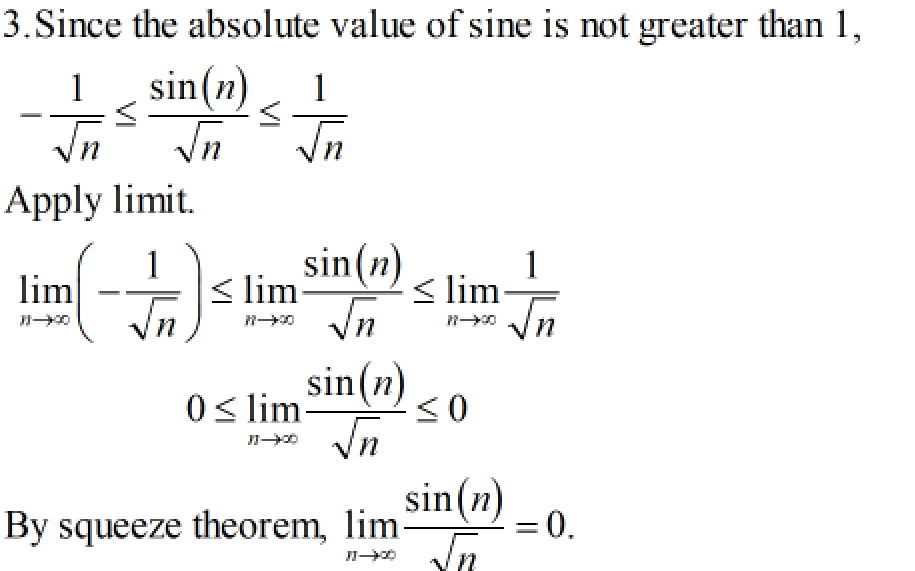
Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 3 steps with 5 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Similar questions
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS