(3) V3 = R³ and U3 = {(a + b, b, a + b): a, b ≤ R}. (4) V₁ = R³ and U₁ = (5) V5 = R³ and U5 = {(a, b, c) € R³ : a+b+c = 0 and b + c=0}. {(a, b, c) € R³ : a =0 or b =0 or c = 0}.
(3) V3 = R³ and U3 = {(a + b, b, a + b): a, b ≤ R}. (4) V₁ = R³ and U₁ = (5) V5 = R³ and U5 = {(a, b, c) € R³ : a+b+c = 0 and b + c=0}. {(a, b, c) € R³ : a =0 or b =0 or c = 0}.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
could you please help me with 3 and 4 and can you please provide explanations
![2. Below is a list V₂ of vector spaces over R. You are given subsets U₁ V₁. Decide which
of these are subspaces. Justify your answers by giving a proof or a counter-example in each
case.
(1) V₁ = R¹ and U₁ = { (ao, a₁, a2, A3) € R4 | Σ²_o a₁ = 0}.
i=0
(2) V₂ = R³ and U₂ = { (a, b, c) € R³ | ab= c }.
(3) V3 R³ and U3 =
{(a + b, b, a+b): a, b ≤ R}.
(4) V4 R³ and U₁ = {(a, b, c) € R³: a+b+c = 0 and b + c = 0}.
(5) V5 = R³ and U5 = {(a, b, c) € R³ : a = 0 or b = 0 or c = 0}.
(6) V6 = R[x] is the vector space of polynomials with real coefficients (this was example
3 in the lecture). U6 = {p E R[x] : p(1)=0}.
(7) V₂ = C([0, 1]) is the vector space of continuous functions from the interval [0, 1] to R.
U+= {f e C([0, 1]) : fồf(z) - xdz =0}.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F4061eb31-6ba2-4539-9b51-dd7b05481e7e%2F833cdd16-57a7-4882-858e-64d3a8ff37e6%2Fzz0et4_processed.png&w=3840&q=75)
Transcribed Image Text:2. Below is a list V₂ of vector spaces over R. You are given subsets U₁ V₁. Decide which
of these are subspaces. Justify your answers by giving a proof or a counter-example in each
case.
(1) V₁ = R¹ and U₁ = { (ao, a₁, a2, A3) € R4 | Σ²_o a₁ = 0}.
i=0
(2) V₂ = R³ and U₂ = { (a, b, c) € R³ | ab= c }.
(3) V3 R³ and U3 =
{(a + b, b, a+b): a, b ≤ R}.
(4) V4 R³ and U₁ = {(a, b, c) € R³: a+b+c = 0 and b + c = 0}.
(5) V5 = R³ and U5 = {(a, b, c) € R³ : a = 0 or b = 0 or c = 0}.
(6) V6 = R[x] is the vector space of polynomials with real coefficients (this was example
3 in the lecture). U6 = {p E R[x] : p(1)=0}.
(7) V₂ = C([0, 1]) is the vector space of continuous functions from the interval [0, 1] to R.
U+= {f e C([0, 1]) : fồf(z) - xdz =0}.
Expert Solution
Step 1: Condition for a subspace
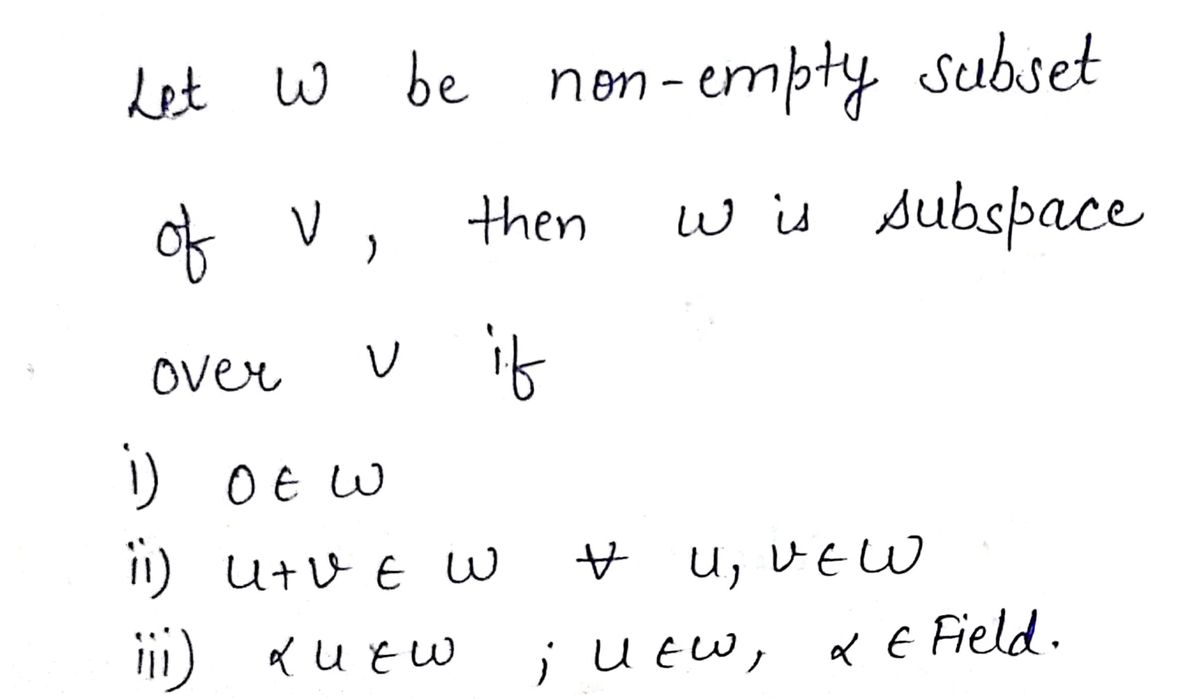
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

