(2t+2)8(t-1) =. cos (t) 6(t+) S (e*) o(t+1)dt S (?-2) 8(2-t) dt
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:Robert L. Boylestad
Chapter1: Introduction
Section: Chapter Questions
Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...
Related questions
Concept explainers
Three-Phase Transformers
Three-segment transformers are a type of transformer used to transform voltages of electrical systems into three ranges. Two type transformers are shell-type transformer and core type transformer. In brief, it could be described because of the exquisite kinds of configurations.
Transformer
Ever since electricity has been created, people have started using it in its entirety. We see many types of Transformers in the neighborhoods. Some are smaller in size and some are very large. They are used according to their requirements. Many of us have seen the electrical transformer but they do not know what work they are engaged in.
Question
100%
Please answer the following :
![Certainly! Here is the transcription and explanation of each item in the image as it would appear on an educational website:
---
### Mathematical Expressions Involving the Dirac Delta Function
1. **Expression 1:**
\[
(2t + 2) \delta(t - 1) = \underline{\hspace{20em}}
\]
This expression involves the Dirac delta function, \(\delta(t - 1)\), which is non-zero only when \(t = 1\). The term \(2t + 2\) is evaluated at this point.
2. **Expression 2:**
\[
\cos(t) \delta \left( t + \frac{\pi}{2} \right) = \underline{\hspace{20em}}
\]
Here, the Dirac delta function \(\delta \left( t + \frac{\pi}{2} \right)\) indicates that the cosine function should be evaluated at \(t = -\frac{\pi}{2}\).
3. **Integral 1:**
\[
\int_{-\infty}^{\infty} \left( e^{t+1} \right) \delta(t + 1) \, dt = \underline{\hspace{20em}}
\]
This integral signifies that the exponential function \(e^{t+1}\) should be evaluated where the delta function \(\delta(t + 1)\) is non-zero, i.e., at \(t = -1\).
4. **Integral 2:**
\[
\int_{-\infty}^{\infty} \left( t^2 - 2 \right) \delta(2 - t) \, dt = \underline{\hspace{20em}}
\]
In this integral, the expression \(t^2 - 2\) is evaluated at the point where the delta function \(\delta(2 - t)\) is active, which is at \(t = 2\).
These expressions and integrals are useful in various applications of signal processing and systems analysis, where the Dirac delta function is often used to model impulse inputs.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fad16e748-6a7d-4448-b034-0f7e391345fb%2F96519ba3-0bb3-481d-b1bf-2f068c2efb50%2F0fpkmf_processed.jpeg&w=3840&q=75)
Transcribed Image Text:Certainly! Here is the transcription and explanation of each item in the image as it would appear on an educational website:
---
### Mathematical Expressions Involving the Dirac Delta Function
1. **Expression 1:**
\[
(2t + 2) \delta(t - 1) = \underline{\hspace{20em}}
\]
This expression involves the Dirac delta function, \(\delta(t - 1)\), which is non-zero only when \(t = 1\). The term \(2t + 2\) is evaluated at this point.
2. **Expression 2:**
\[
\cos(t) \delta \left( t + \frac{\pi}{2} \right) = \underline{\hspace{20em}}
\]
Here, the Dirac delta function \(\delta \left( t + \frac{\pi}{2} \right)\) indicates that the cosine function should be evaluated at \(t = -\frac{\pi}{2}\).
3. **Integral 1:**
\[
\int_{-\infty}^{\infty} \left( e^{t+1} \right) \delta(t + 1) \, dt = \underline{\hspace{20em}}
\]
This integral signifies that the exponential function \(e^{t+1}\) should be evaluated where the delta function \(\delta(t + 1)\) is non-zero, i.e., at \(t = -1\).
4. **Integral 2:**
\[
\int_{-\infty}^{\infty} \left( t^2 - 2 \right) \delta(2 - t) \, dt = \underline{\hspace{20em}}
\]
In this integral, the expression \(t^2 - 2\) is evaluated at the point where the delta function \(\delta(2 - t)\) is active, which is at \(t = 2\).
These expressions and integrals are useful in various applications of signal processing and systems analysis, where the Dirac delta function is often used to model impulse inputs.
Expert Solution
Step 1
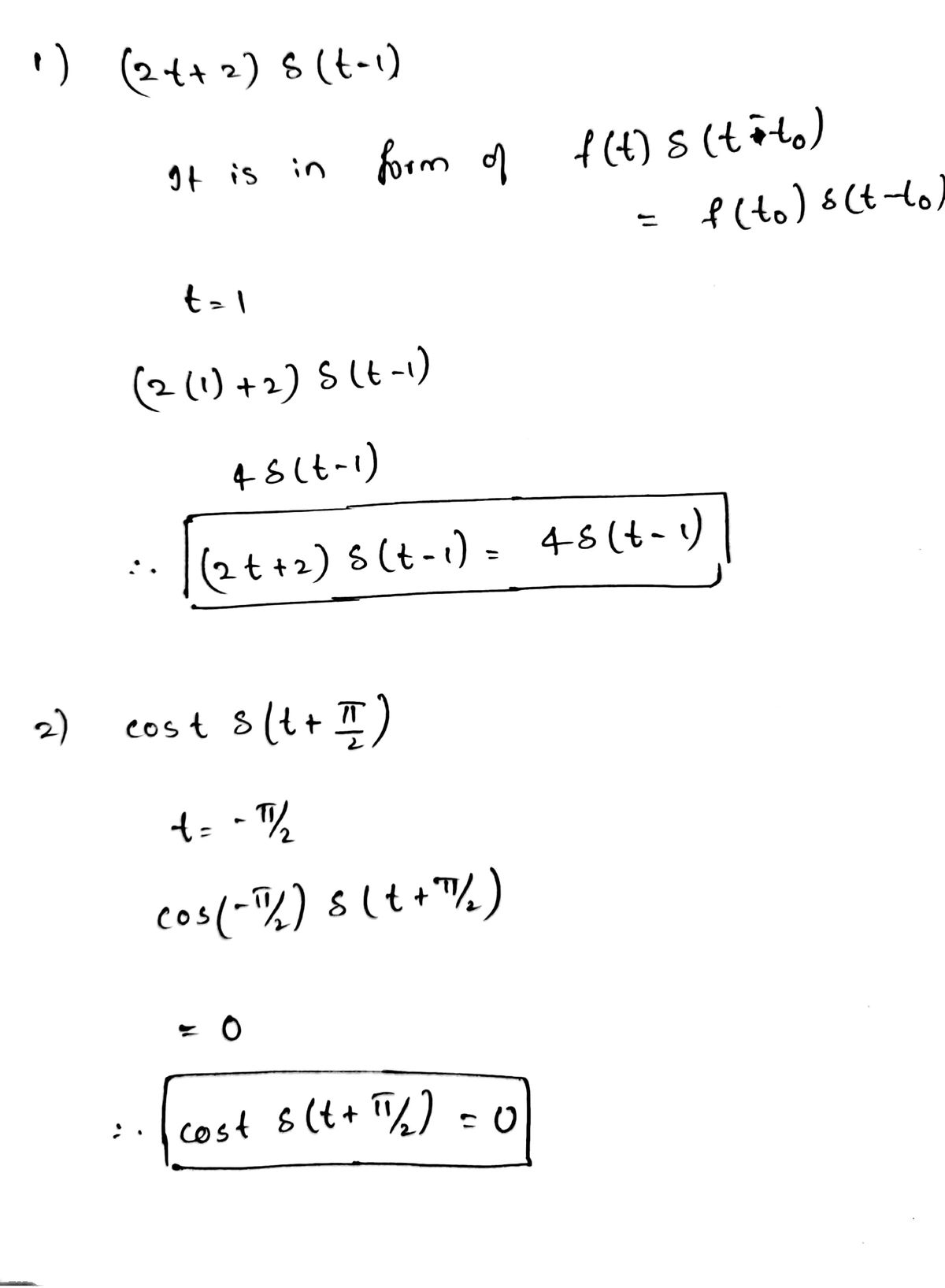
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, electrical-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON

Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning

Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education

Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON

Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning

Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education

Fundamentals of Electric Circuits
Electrical Engineering
ISBN:
9780078028229
Author:
Charles K Alexander, Matthew Sadiku
Publisher:
McGraw-Hill Education

Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:
9780134746968
Author:
James W. Nilsson, Susan Riedel
Publisher:
PEARSON

Engineering Electromagnetics
Electrical Engineering
ISBN:
9780078028151
Author:
Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:
Mcgraw-hill Education,